Kỳ thi THPT Quốc gia sắp đến gần, vì vậy Khoa Cử muốn chia sẻ đến với các độc giả của chúng tôi về chuyên đề số phức qua bài viết ngày hôm nay. Bài viết này sẽ có chuyên đề số phức có lời giải cũng như chuyên đề số phức nâng cao trong môn toán lớp 12, đồng thời đưa ra các chọn lọc giúp bạn ôn tập và rèn luyện kỹ năng giải toán. Hãy cùng tìm hiểu bài viết này ngay sau đây nhé!
I. LÝ THUYẾT VỀ CHUYÊN ĐỀ SỐ PHỨC LUYỆN THI ĐẠI HỌC
Để có thể làm được các dạng bài tập liên quan đến chuyên đề số phức luyện thi đại học một cách dễ dàng nhất thì chúng ta cần phải nắm vững và thật chắc các công thức trong dạng cũng như tính chất này như sau:
1. ĐỊNH NGHĨA SỐ PHỨC
| o Một số phức là một biểu thức dạng $z=a+bi$ với $a,b\in \mathbb{R}$ và ${{i}^{2}}=-1$.
o $i$ được gọi là đơn vị ảo, $a$được gọi là phần thực và $b$được gọi là phần ảo của số phức $z=a+bi$. Tập hợp các số phức được kí hiệu là $\mathbb{C}$. $\mathbb{C}=\left\{ a+bi/a,b\in \mathbb{R};{{i}^{2}}=-1 \right\}$. o Chú ý: – Khi phần ảo $b=0\Leftrightarrow z=a$ là số thực. – Khi phần thực $a=0\Leftrightarrow z=bi\Leftrightarrow z$là số thuần ảo. – Số $0=0+0i$ vừa là số thực, vừa là số ảo. o Hai số phức bằng nhau: $a+bi=c+di\Leftrightarrow \left\{ \begin{matrix}a=c \\b=d \\\end{matrix} \right.\text{ }$với $a,b,c,d\in \mathbb{R}$. o Hai số phức ${{z}_{1}}=a+bi;\text{ }{{z}_{2}}=-a-bi$ được gọi là hai số phức đối nhau. |
2. SỐ PHỨC LIÊN HỢP
| Số phức liên hợp của $z=a+bi$ với $a,b\in \mathbb{R}$ là $a-bi$ và được kí hiệu bởi $\overline{z}$ .
Một số tính chất của số phức liên hợp: a) $\overline{\overline{z}}=z$$$ b)$\overline{z+z’}=\overline{z}+\overline{z’}$ c) $\overline{z-z’}=\overline{z}-\overline{z’}$ c) $\overline{z.z’}=\overline{z}.\overline{z’}$ d) $\overline{\left( \frac{z}{{{z}’}} \right)}=\frac{\overline{z}}{\overline{{{z}’}}}$ $z$ là số thực $\Leftrightarrow z=\overline{z}$ ; $z$ là số thuần ảo $\Leftrightarrow z=-\overline{z}$. |
3. BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
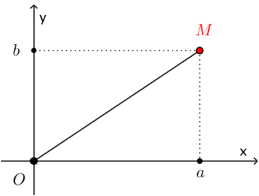
| Trong mặt phẳng phức Oxy ( Ox là trục thực, Oy là trục ảo ), số phức $z=a+bi$ với $a,b\in \mathbb{R}$được biểu diễn bằng điểm $M\left( a;b \right)$. |
4. MODULE CỦA SỐ PHỨC
| o Môđun của số phức $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$ là $\overline{z}=\sqrt{{{a}^{2}}+{{b}^{2}}}$ .
o Như vậy, môđun của số phức $z$ là $\overline{z}$ chính là khoảng cách từ điểm M biểu diễn số phức $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$đến gốc tọa độ O của mặt phẳng phức là:$\left| \overrightarrow{OM} \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{z\overline{z}}$ . o Một số tính chất của môđun: $\begin{align}& \bullet \text{ }\left| z \right|\ge 0;\left| z \right|=0\Leftrightarrow z=0; \\& \bullet \text{ }\left| {{z}^{2}} \right|={{\left| z \right|}^{2}},\text{ }\left| -z \right|=\left| z \right|,\text{ }\left| \overline{z} \right|=\left| z \right| \\& \bullet \text{ }\left| {{z}_{1}}+{{z}_{2}} \right|\le \left| {{z}_{1}} \right|\text{+}\left| {{z}_{2}} \right|\text{ } \\& \bullet \text{ }\left| \left| z \right|-\left| z’ \right| \right|\le \left| z-z’ \right|\le \left| z \right|+\left| z’ \right| \\& \bullet \text{ }\left| {{z}_{1}}.{{z}_{2}} \right|=\left| {{z}_{1}} \right|.\left| {{z}_{2}} \right|\text{ } \\& \bullet \text{ }\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|=\frac{\left| {{z}_{1}} \right|}{\left| {{z}_{2}} \right|} \\\end{align}$
|
5. CÁC PHÉP TOÁN VỚI SỐ PHỨC: CỘNG – TRỪ – NHÂN – CHIA SỐ PHỨC
Cho hai số phức $z=a+bi$; $z’=a’+b’i\text{ }$với $a,b,a’,b’\in \mathbb{R}$và số $k\in \mathbb{R}$.
$\overrightarrow{u}+\overrightarrow{u’}$ biểu diễn số phức $z+z’$. $\overrightarrow{u}-\overrightarrow{u’}$ biểu diễn số phức $z-z’$.
$z.z’=\left( a+bi \right)\left( a’+b’i \right)=\left( a.a’-b.b’ \right)+\left( a.b’+a’.b \right)i$.
Nếu $z\ne 0$thì $\frac{z’}{z}=\frac{z’.\overline{z}}{{{\left| z \right|}^{2}}}$, nghĩa là nếu muốn chia số phức $z’$cho số phức $z\ne 0$ thì ta nhân cả tử và mẫu của thương $\frac{z’}{z}$cho $\overline{z}$.
${{i}^{4k}}=1;\text{ }{{i}^{4k+1}}=i;\text{ }{{i}^{4k+2}}=-1;\text{ }{{i}^{4k+3}}=-i\text{ (k}\in \mathbb{Z})$.. |
Xem thêm: Các dạng bài tập số phức đầy đủ và chi tiết
6. CĂN BẬC HAI CỦA SỐ PHỨC
| Cho số phức $w$. Mỗi số phức z thỏa mãn ${{z}^{2}}=w$ được gọi là một căn thức bậc 2 của$w$ . Mỗi số phức $w\ne 0$ 0 có hai căn bậc hai là hai số phức đối nhau $\left( z\text{ }v\grave{a}z \right).$
o Trường hợp $w$ là số thực ($w=a\in \mathbb{R}$) + Khi $a>0$thì $w$ có hai căn bậc hai là $\sqrt{a}$ và $-\sqrt{a}$. + Khi $a<0$ nên $a=(-a){{i}^{2}}$, do đó $w$ có hai căn bậc hai là $\sqrt{-a}.i$ và $-\sqrt{-a}.i$. Ví dụ: Hai căn bậc 2 của $-1$ là $i$ và $i$ . Hai căn bậc 2 của $-{{a}^{2}}\text{ }(a\ne 0)$ là $ai\text{ }\text{,}-ai$. o Trường hợp $w=a+bi\text{ }(a,b\in \mathbb{R};b\ne 0)$. Cách 1: Gọi $z=x+yi\text{ }(x,y\in \mathbb{R})$là căn bậc 2 của $w$ khi và chỉ khi ${{z}^{2}}=w$, tức là: $\begin{align}& \text{ }{{(x+yi)}^{2}}=a+bi \\& \Leftrightarrow \left\{ \begin{matrix}{{x}^{2}}-{{y}^{2}}=a \\2xy=b \\\end{matrix} \right.\to x=…;y=… \\\end{align}$ Mỗi cặp số thực $\left( x;y \right)$ nghiệm đúng hệ phương trình đó cho ra một căn bậc hai $z=x+yi$ của số phức $w=a+bi$. Cách 2: Có thể biến đổi $w$ thành bình phương của một tổng, nghĩa là $w={{z}^{2}}$. Từ đó kết luận căn bậc hai của $w$ là $z$ và -$z$.. |
7. TÌM MIN-MAX CỦA HÀM MỘT BIẾN
| Sử dụngcác tính chất và các bất đẳng thức về môđun của số phức sau để giải quyết các bài toán min-max:
$\begin{align}& \bullet \text{ }\overline{\overline{z}}=z \\& \bullet \text{ }\overline{z+z’}=\overline{z}+\overline{z’} \\& \bullet \text{ }\overline{z-z’}=\overline{z}-\overline{z’} \\& \bullet \text{ }\overline{z.z’}=\overline{z}.\overline{z’} \\& \bullet \text{ }\overline{\left( \frac{z}{z’} \right)}=\frac{\overline{z}}{\overline{z’}} \\\end{align}$ $\begin{align}& \bullet \text{ }\left| z \right|\ge 0;\left| z \right|=0\Leftrightarrow z=0; \\& \bullet \text{ }\left| {{z}^{2}} \right|={{\left| z \right|}^{2}},\text{ }\left| -z \right|=\left| z \right|,\text{ }\left| \overline{z} \right|=\left| z \right| \\& \bullet \text{ }\left| {{z}_{1}}+{{z}_{2}} \right|\le \left| {{z}_{1}} \right|\text{+}\left| {{z}_{2}} \right|\text{ } \\& \bullet \text{ }\left| \left| z \right|-\left| z’ \right| \right|\le \left| z-z’ \right|\le \left| z \right|+\left| z’ \right| \\& \bullet \text{ }\left| {{z}_{1}}.{{z}_{2}} \right|=\left| {{z}_{1}} \right|.\left| {{z}_{2}} \right|\text{ } \\& \bullet \text{ }\left| \frac{{{z}_{1}}}{{{z}_{2}}} \right|=\frac{\left| {{z}_{1}} \right|}{\left| {{z}_{2}} \right|} \\\end{align}$ Kết hợp sử dụng các bất đẳng thức liên hệ giữa trung bình cộng và trung bình nhân, BĐT Bunhia- Cốpxki. § Bất đẳng thức Bunhiacopxki :Cho các số thực $a,b,x,y$ ta luôn có ${{\left( ax+by \right)}^{2}}\le \left( {{a}^{2}}+{{b}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}} \right)$ . Dấu = xảy ra $\Leftrightarrow \frac{a}{x}=\frac{b}{y}$ § Bất đẳng thức Vectơ : Cho 2 vecto $\overrightarrow{u}\left( x;y \right)$ và $\overrightarrow{v}\left( x’;y’ \right)$ ta luôn có $\left| \overrightarrow{u} \right|+\left| \overrightarrow{v} \right|\ge \left| \overrightarrow{u+v} \right|$ $\Leftrightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}+\sqrt{x{{‘}^{2}}+y{{‘}^{2}}}\ge \sqrt{{{\left( x-x’ \right)}^{2}}+{{\left( y-y’ \right)}^{2}}}$ Dấu = xảy ra $\Leftrightarrow \frac{x}{x’}=\frac{y}{y’}<0$. |
II. BÀI TẬP MẪU CHUYÊN ĐỀ SỐ PHỨC
Khi đã nắm chắc được các lý thuyết liên quan đến các dạng thì chúng ta cần phải làm thêm một số bài tập mẫu để có thể hiểu rõ hơn chương số phức này ngay bên dưới đây:
Dạng 1: SỐ PHỨC LIÊN HỢP
Bài tập 1: Cho $z$ và $\overset{\_}{\mathop{z}}\,$ là số phức liên hợp của $z$ . Biết $\frac{z}{{{\left( \overline{z} \right)}^{2}}}\in \mathbb{R}$ và $\left| z-\overline{z} \right|=2\sqrt{3}$.Tìm $\left| z \right|$
Giải :
Gọi $z=a+bi\,\,\,\left( a,b\in \mathbb{R} \right)\,\,\,\,\,\,\Rightarrow \overset{\_}{\mathop{z}}\,=a-bi$.
Ta có :$\left| z-\overline{z} \right|=\left| \left( a+bi \right)-\left( a-bi \right) \right|=\left| 2bi \right|=2\sqrt{3}\Rightarrow {{b}^{2}}=3$.
$z.\overset{\_}{\mathop{z}}\,\in \mathbb{R}\Rightarrow {{\left( z.\overline{z} \right)}^{2}}\in \mathbb{R}$. Ta có: $\frac{z}{{{\left( \overline{z} \right)}^{2}}}=\frac{z}{{{\left( \overline{z} \right)}^{2}}}.1=\frac{z}{{{\left( \overline{z} \right)}^{2}}}.\frac{{{z}^{2}}}{{{z}^{2}}}=\frac{{{z}^{3}}}{{{\left( z.\overline{z} \right)}^{2}}}\in \mathbb{R}\,\,\,\,\Rightarrow {{z}^{3}}\in \mathbb{R}$.
Mà ${{z}^{3}}={{a}^{3}}+3{{a}^{2}}bi+3a{{\left( bi \right)}^{2}}+{{\left( bi \right)}^{3}}={{a}^{3}}-3a{{b}^{2}}+\left( 3{{a}^{2}}b-{{b}^{3}} \right)i$
![]()
Bài tập 2: Tìm phần thực, phần ảo, số phức liên hợp và tính môđun của số phức$z$:
$a)\text{ }z=\left( 2+4i \right)+2i\left( 1-3i \right).$ $b)\text{ }z=\left( 2-4i \right)\left( 5+2i \right)+\frac{4-5i}{2+i}$.
Giải:
$\text{ a) }z=\left( 2+4i \right)+2i\left( 1-3i \right)=2+4i+2i-6{{i}^{2}}=2+6i+6=8+6i$.
$\Rightarrow $ Phần thực: 8 ; Phần ảo: 6 ; Số phức liên hợp: $\overline{z}=8-6i$.
Môđun $\left| z \right|=\sqrt{{{8}^{2}}+{{6}^{2}}}=10$.
$\begin{align}& \text{b) }z=\left( 2-4i \right)\left( 5+2i \right)+\frac{4-5i}{2+i}=10+4i-20i-8{{i}^{2}}+\frac{\left( 4-5i \right)\left( 2-i \right)}{{{2}^{2}}+{{1}^{2}}} \\& \text{ }=18-16i+\frac{8-14i-5}{5}=\frac{93}{5}-\frac{94}{5}i. \\\end{align}$
$\Rightarrow $ Phần thực:$\frac{93}{5}$ ; Phần ảo: $\frac{94}{5}$; Số phức liên hợp: $\overline{z}=\frac{93}{5}+\frac{94}{5}i$.
Môđun $\left| z \right|=\sqrt{{{\left( \frac{93}{5} \right)}^{2}}+{{\left( \frac{94}{5} \right)}^{2}}}=\frac{\sqrt{17485}}{5}$.
Dạng 2: BIỂU DIỄN HÌNH HỌC CỦA SỐ PHỨC
Câu 1. Giả sử M là điểm trên mặt phẳng phức biểu diễn số phức $z$. Tìm tập hợp các điểm M thỏa mãn một trong các điều kiện sau đây:
a) $\left| z-1+i \right|=2$ b) $\left| z+1-3i \right|\le 4$ c) $\left| 2+z \right|=\left| z-i \right|$
Giải:
Đặt $z=x+yi\text{ }(x,y\in \mathbb{R})$ được biểu diễn bởi điểm $M\left( x;y \right)$
a) Xét hệ thức: $\left| z-1+i \right|=2$.
$\begin{align}& \Leftrightarrow \left| \left( x1 \right)+\left( y+1 \right)i \right|=2 \\& \Leftrightarrow \sqrt{{{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}}=2. \\& \Leftrightarrow {{\left( x-1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=4. \\\end{align}$
Tập hợp các điểm $M\left( z \right)$ trên mặt phẳng tọa độ biểu diễn số phức $z$ thỏa mãn (1) là đường tròn có tâm tại $I\left( 1;-1 \right)$ và bán kính$R=2$ .
b) Xét hệ thức :$\left| z+1-3i \right|\le 4\Leftrightarrow \left| \left( x+1 \right)+\left( y-3 \right)i \right|\le 4$
$\text{ }\Leftrightarrow \sqrt{{{\left( x+1 \right)}^{2}}+\text{ }{{\left( y-1 \right)}^{2}}}\le 4$
$\text{ }\Leftrightarrow {{\left( x+1 \right)}^{2}}+\text{ }{{\left( y-1 \right)}^{2}}\le \text{16}.$
Vậy tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn số phức $z$ là hình tròn có tâm là$\left( -1;1 \right)$; bán kính $r=4$ .
Nhận xét: Tập hợp các điểm biểu diễn số phức $z$ thỏa mãn điều kiện: $\left| z+1-3i \right|\ge 4$ là tập hình các điểm nằm trên và nằm ngoài đường tròn có tâm là$\left( -1;1 \right)$ ; bán kính $r=4$ .
c) Xét hệ thức: $\left| 2+z \right|=\left| z-i \right|$
$\begin{array}{*{35}{l}}\Leftrightarrow \left| \left( x+2 \right)+yi \right|=\left| x+\left( y-1 \right)i \right| \\\Leftrightarrow {{\left( x+2 \right)}^{2}}+{{y}^{2}}={{x}^{2}}+{{\left( y-1 \right)}^{2}} \\\Leftrightarrow 4x+2y+3=0. \\\end{array}$
Vậy tập hợp các điểm M là đường thẳng
$4x+2y+3=0.$
Nhận xét: Đường thẳng $4x+2y+3=0$ chính là đường trung trực của đoạn AB.
Dạng 3: MODULE CỦA SỐ PHỨC
Tính môđun của số phức $z$ biết $z\ne \left| z \right|$ và $\frac{1}{\left| z \right|-z}$ có phần thực bằng $4.$
Giải:
Cách 1: Giả sử $z=a+bi$ $\left( a,\text{ }b\in \mathbb{R} \right)$.
Ta có $\frac{1}{\left| z \right|-z}=\frac{1}{\sqrt{{{a}^{2}}+{{b}^{2}}}-a-bi}$
$=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a+bi}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}+\frac{b}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}i.$
Theo giả thiết: $\frac{1}{\left| z \right|-z}$ có phần thực bằng 4 nên $\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}=4$
$\Leftrightarrow \frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{2\left( {{a}^{2}}+{{b}^{2}} \right)-2a\sqrt{{{a}^{2}}+{{b}^{2}}}}=4\Leftrightarrow \frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{2\sqrt{{{a}^{2}}+{{b}^{2}}}\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}=4$
$\Leftrightarrow \frac{1}{2\sqrt{{{a}^{2}}+{{b}^{2}}}}=4\Leftrightarrow \sqrt{{{a}^{2}}+{{b}^{2}}}=\frac{1}{8}\Rightarrow \left| z \right|=\frac{1}{8}.$
Cách 2: Nếu $z=a+bi$ thì $z+\bar{z}=2a$.
Áp dụng: $\frac{1}{\left| z \right|-z}$ có phần thực bằng $4\Rightarrow $ $\frac{1}{\left| z \right|-z}+\overline{\frac{1}{\left| z \right|-z}}=8$
$\Leftrightarrow \frac{1}{\left| z \right|-z}+\frac{1}{\left| z \right|-\bar{z}}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)+z.\bar{z}}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)+{{\left| z \right|}^{2}}}=8$
$\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{2{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{\left| z \right|\left( 2\left| z \right|-z-\bar{z} \right)}=8\Leftrightarrow \frac{1}{\left| z \right|}=8\Leftrightarrow \left| z \right|=\frac{1}{8}.$
| Nhận xét:
Trong bài toán tìm thuộc tính của số phức $z$ thỏa mãn điều kiện K cho trước, nếu K là thuần $z$ (tất cả đều$z$ ) hoặc thuần $\overline{z}$ thì đó là bài toán giải phương trình bậc nhất (phép cộng, trừ, nhân, chia số phức) với ẩn $z$ hoặc $\overline{z}$. Còn nếu chứa hai loại trở lên ($z$ , $\overline{z}$,$\left| z \right|$) thì ta sẽ gọi $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$. Từ đó sử dụng các phép toán trên số phức để đưa về hai số phức bằng nhau để giải.. |
Dạng 4: CÁC PHÉP TOÁN VỚI SỐ PHỨC: CỘNG – TRỪ – NHÂN – CHIA SỐ PHỨC
Tính môđun của số phức $z$ biết $z\ne \left| z \right|$ và $\frac{1}{\left| z \right|-z}$ có phần thực bằng $4.$
Giải:
Cách 1: Giả sử $z=a+bi$ $\left( a,\text{ }b\in \mathbb{R} \right)$.
Ta có $\frac{1}{\left| z \right|-z}=\frac{1}{\sqrt{{{a}^{2}}+{{b}^{2}}}-a-bi}$
$=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a+bi}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}=\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}+\frac{b}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}i.$
Theo giả thiết: $\frac{1}{\left| z \right|-z}$ có phần thực bằng 4 nên $\frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{{{\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}^{2}}+{{b}^{2}}}=4$
$\Leftrightarrow \frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{2\left( {{a}^{2}}+{{b}^{2}} \right)-2a\sqrt{{{a}^{2}}+{{b}^{2}}}}=4\Leftrightarrow \frac{\sqrt{{{a}^{2}}+{{b}^{2}}}-a}{2\sqrt{{{a}^{2}}+{{b}^{2}}}\left( \sqrt{{{a}^{2}}+{{b}^{2}}}-a \right)}=4$
$\Leftrightarrow \frac{1}{2\sqrt{{{a}^{2}}+{{b}^{2}}}}=4\Leftrightarrow \sqrt{{{a}^{2}}+{{b}^{2}}}=\frac{1}{8}\Rightarrow \left| z \right|=\frac{1}{8}.$
Cách 2: Nếu $z=a+bi$ thì $z+\bar{z}=2a$.
Áp dụng: $\frac{1}{\left| z \right|-z}$ có phần thực bằng $4\Rightarrow $ $\frac{1}{\left| z \right|-z}+\overline{\frac{1}{\left| z \right|-z}}=8$
$\Leftrightarrow \frac{1}{\left| z \right|-z}+\frac{1}{\left| z \right|-\bar{z}}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)+z.\bar{z}}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)+{{\left| z \right|}^{2}}}=8$
$\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{2{{\left| z \right|}^{2}}-\left| z \right|\left( z+\bar{z} \right)}=8\Leftrightarrow \frac{2\left| z \right|-z-\bar{z}}{\left| z \right|\left( 2\left| z \right|-z-\bar{z} \right)}=8\Leftrightarrow \frac{1}{\left| z \right|}=8\Leftrightarrow \left| z \right|=\frac{1}{8}.$
| Nhận xét:
Trong bài toán tìm thuộc tính của số phức $z$ thỏa mãn điều kiện K cho trước, nếu K là thuần $z$ (tất cả đều$z$ ) hoặc thuần $\overline{z}$ thì đó là bài toán giải phương trình bậc nhất (phép cộng, trừ, nhân, chia số phức) với ẩn $z$ hoặc $\overline{z}$. Còn nếu chứa hai loại trở lên ($z$ , $\overline{z}$,$\left| z \right|$) thì ta sẽ gọi $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$. Từ đó sử dụng các phép toán trên số phức để đưa về hai số phức bằng nhau để giải.. |
Dạng 5: CĂN BẬC HAI CỦA SỐ PHỨC
Cho số phức $z=3+2i$. Tìm môđun số phức $w=zi+\overline{z}\left( 1+2i \right)$.
Giải:
$\begin{align}& w=zi+\overline{z}\left( 1+2i \right)=(3+2i)i+(3-2i)(1+2i) \\& \text{ }=3i-2+3+6i-2i+4=5+7i \\\end{align}$.
Vậy $\left| w \right|=\sqrt{{{5}^{2}}+{{7}^{2}}}=\sqrt{74}$.
Dạng 6:TÌM MIN-MAX CỦA HÀM MỘT BIẾN
Cho các số phức $z$ thỏa mãn $\left| z \right|={{m}^{2}}+2m+5$, với $m$ là tham số thực. Biết rằng tập hợp các điểm biểu diễn các số phức $w=\left( 3-4i \right)z-2i$ là một đường tròn. Bán kính nhỏ nhất của đường tròn đó bằng?
Giải :
Cách 1 : Gọi $w=x+yi$.
Từ giả thiết, ta có $x+yi=\left( 3-4i \right)z-2i\Rightarrow z=\frac{x+\left( y+2 \right)i}{3-4i}=\frac{3x-4y-8}{25}+\frac{4x+3y+6}{25}.i$
$\Rightarrow \left| z \right|=\frac{\sqrt{{{\left( 3x-4y-8 \right)}^{2}}+{{\left( 4x+3y+6 \right)}^{2}}}}{25}$.
Mà $\left| z \right|={{m}^{2}}+2m+5\Leftrightarrow {{\left( 3x-4y-8 \right)}^{2}}+{{\left( 4x+3y+6 \right)}^{2}}={{25}^{2}}\left( {{m}^{2}}+2m+25 \right)$
$\Leftrightarrow {{x}^{2}}+{{y}^{2}}+4y+4=25{{\left[ {{\left( m+1 \right)}^{2}}+4 \right]}^{2}}\Leftrightarrow {{x}^{2}}+{{\left( y+2 \right)}^{2}}=25{{\left[ {{\left( m+1 \right)}^{2}}+4 \right]}^{2}}\ge 400={{20}^{2}}.$
Vậy bán kính nhỏ nhất của đường tròn đó là 20. Dấu $”=”$ xảy ra khi $m=-1$.
Cách 2: Từ giả thiết, ta có $w+2i=\left( 3-4i \right)z$.
Lấy môđun hai vế, ta được $\left| w+2i \right|=\left| 3-4i \right|.\left| z \right|=5.\left( {{m}^{2}}+2m+5 \right)=5\left[ {{\left( m+1 \right)}^{2}}+4 \right]\ge 20.$
Như vậy, bên trên là tất tần tật những chuyên đề số phức có lời giải trong toán 12 rất quan trọng mà bạn nên ghi nhớ và hiểu thật rõ để có thể vượt qua được kỳ thi THPT Quốc Gia sắp tới. Mong rằng qua bài viết trên đã có thể giúp bạn dễ dàng hơn trong các chuyên đề số phức luyện thi đại học và đạt được điểm cao trong học tập nhé!
Xem thêm:
Lý thuyết và dạng bài tập mẫu của max min số phức
Cách giải và bài tập mẫu cực trị số phức