Bài viết sau đây giới thiệu đến các bạn lý thuyết và bài tập mẫu cộng, trừ và nhân số phức, cách nhân 2 số phức để các bạn tham khảo. Khoa Cử hy vọng với những chia sẻ này sẽ hỗ trợ bạn đọc học tốt phần các dạng bài tập về số phức môn Toán lớp 12!
I. CÁCH GIẢI CÁC DẠNG CỘNG, TRỪ VÀ NHÂN SỐ PHỨC
Số phức $z=a+bi$ có phần thực là $a,$ phần ảo là $b.$
Số phức liên hợp $\bar{z}=a-bi$ và cần nhớ ${{i}^{2}}=-1.$
Số phức $z=a+bi$ có điểm biểu diễn là $M(a;b).$
số phức liên hợp $\bar{z}=a-bi$ có điểm biểu diễn $N(a;-b).$
Hai điểm $M$và $N$đối xứng nhau qua trục hoành $Ox.$
- $\bar{\bar{z}}=z;$ $\overline{z+{z}’}=\bar{z}+\overline{{{z}’}};$$\overline{z-{z}’}=\bar{z}-\overline{{{z}’}};$
$\bar{z}.\overline{{{z}’}}=\overline{z.{z}’};$ $\overline{\left( \frac{z}{{{z}’}} \right)}=\frac{{\bar{z}}}{{{\bar{z}}’}};$ $z.\bar{z}={{a}^{2}}+{{b}^{2}}$
Hai số phức bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đun của số phức $z$ là: $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
- $\left| z.{z}’ \right|=\left| z \right|\left| {{z}’} \right|$ · $\left| \frac{z}{{{z}’}} \right|=\frac{\left| z \right|}{\left| {{z}’} \right|}$
- $\left| \left| z \right|-\left| {{z}’} \right| \right|\le \left| z+{z}’ \right|\le \left| z \right|+\left| {{z}’} \right|$ · $\left| \left| z \right|-\left| {{z}’} \right| \right|\le \left| z-{z}’ \right|\le \left| z \right|+\left| {{z}’} \right|$
– Phép cộng hai số phức Cho số phức ${{z}_{1}}=a+b.i$ và ${{z}_{2}}=c+d.i$. Khi đó ${{z}_{1}}+{{z}_{2}}=\left( a+b.i \right)+\left( c+d.i \right)=\left( a+c \right)+\left( b+d \right).i.$
– Phép trừ hai số phức ${{z}_{1}}-{{z}_{2}}=\left( a+b.i \right)-\left( c+d.i \right)=\left( a-c \right)+\left( b-d \right).i.$
– Phép nhân hai số phức ${{z}_{1}}.{{z}_{2}}=\left( a+b.i \right).\left( c+d.i \right)=\left( ac-bd \right)+\left( ad+bc \right).i.$
$k.z=k.(a+bi)=ka+kbi$
II. BÀI TẬP MẪU CÁC DẠNG CỘNG, TRỪ VÀ NHÂN SỐ PHỨC
Câu 1: Khẳng định nào sau đây là sai
Cho số phức $z$ khác $0$. Khẳng định nào sau đây là sai?
A. $\frac{z}{{\bar{z}}}$là số thuần ảo. B. $z.\bar{z}$ là số thực. C. $z+\bar{z}$ là số thực. D. $z-\bar{z}$là số ảo.
Lời giải
Đặt $z=a+bi,\text{ }\left( {{a}_{1}},{{b}_{1}}\in \mathbb{R} \right)\Rightarrow \bar{z}=a-bi$.
$\frac{z}{{\bar{z}}}=\frac{a+bi}{a-bi}=\frac{{{\left( a+bi \right)}^{2}}}{\left( a-bi \right)\left( a+bi \right)}=\frac{\left( {{a}^{2}}-{{b}^{2}} \right)+2ab.i}{{{a}^{2}}+{{b}^{2}}}=\frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}+\frac{2ab}{{{a}^{2}}+{{b}^{2}}}.i$ chỉ là số thuần ảo
$\Leftrightarrow a=\pm b$.
Câu 2: Tìm giá trị của $\left| 2{{z}_{1}}-{{z}_{2}} \right|$
Cho hai số phức ${{z}_{1}}$, ${{z}_{2}}$ thỏa mãn các điều kiện $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=2$ và $\left| {{z}_{1}}+2{{z}_{2}} \right|=4$. Giá trị của $\left| 2{{z}_{1}}-{{z}_{2}} \right|$ bằng
A. $2\sqrt{6}$. B. $\sqrt{6}$. C. $3\sqrt{6}$. D. $8$.
Lời giải
Giả sử ${{z}_{1}}=a+bi$, ($a$, $b\in \mathbb{R}$); ${{z}_{2}}=c+di$, ($c$, $d\in \mathbb{R}$).
Theo giả thiết ta có:
$\left\{ \begin{align}& \left| {{z}_{1}} \right|=2 \\& \left| {{z}_{2}} \right|=2 \\& \left| {{z}_{1}}+2{{z}_{2}} \right|=4 \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align}& {{a}^{2}}+{{b}^{2}}=4 \\& {{c}^{2}}+{{d}^{2}}=4 \\& {{\left( a+2c \right)}^{2}}+{{\left( b+2d \right)}^{2}}=16 \\\end{align} \right.$$\Leftrightarrow \left\{ \begin{align}& {{a}^{2}}+{{b}^{2}}=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \\& {{c}^{2}}+{{d}^{2}}=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \\& {{a}^{2}}+{{b}^{2}}+4\left( {{c}^{2}}+{{d}^{2}} \right)+4\left( ac+bd \right)=16\,\,\,\,\,\left( 3 \right) \\\end{align} \right.$
Thay $\left( 1 \right)$,$\left( 2 \right)$vào $\left( 3 \right)$ ta được $ac+bd=-1$ $\left( 4 \right)$.
Ta có $\left| 2{{z}_{1}}-{{z}_{2}} \right|=$$\sqrt{{{\left( 2a-c \right)}^{2}}+{{\left( 2b-d \right)}^{2}}}$ $=\sqrt{4\left( {{a}^{2}}+{{b}^{2}} \right)+\left( {{c}^{2}}+{{d}^{2}} \right)-4\left( ac+bd \right)}$ $\left( 5 \right)$.
Thay $\left( 1 \right)$,$\left( 2 \right)$,$\left( 4 \right)$ vào $\left( 5 \right)$ ta có $\left| 2{{z}_{1}}-{{z}_{2}} \right|=2\sqrt{6}$.
Câu 3: Có bao nhiêu số phức $z$ thỏa mãn điều kiện
Có bao nhiêu số phức $z$ thỏa mãn $\left| z-(2+i) \right|=\sqrt{10}$và $z.\overline{z}=25$.
A. $2$. B. $3$. C. $1$. D. $4$.
Lời giải
Gọi số phức cần tìm là $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$.
Ta có: $z.\overline{z}={{\left| z \right|}^{2}}={{a}^{2}}+{{b}^{2}}=25\text{ (1)}$.
Lại có: $\text{ }\left| z-(2+i) \right|=\sqrt{10}\Leftrightarrow \left| a-2+(b-1)i \right|=\sqrt{10}$
$\begin{align}& \text{ }\Leftrightarrow \sqrt{{{(a-2)}^{2}}+{{(b-1)}^{2}}}=\sqrt{10} \\& \text{ }\Leftrightarrow {{(a-2)}^{2}}+{{(b-1)}^{2}}=10 \\& \text{ }\Leftrightarrow {{a}^{2}}+{{b}^{2}}-4a-2b+5=10\text{ (2)} \\\end{align}$
Thay vào ta được: $25-4a-2b+5=10\Leftrightarrow b=-2a+10$.
Nên$\text{ }{{a}^{2}}+{{b}^{2}}=25\Leftrightarrow {{a}^{2}}+{{(-2a+10)}^{2}}=25$
$\Leftrightarrow 5{{a}^{2}}-40a+75=0\Leftrightarrow \left[ \begin{matrix}a=5 \\a=3 \\\end{matrix} \right.\Leftrightarrow \left[ \begin{matrix}b=0 \\b=4 \\\end{matrix} \right.$
Vậy có 2 số phức $z$ thoả mãn là $z=5$ và $z=3+4i$.
Xem thêm: Cách giải và bài tập mẫu chia 2 số phức
Câu 4: Tính giá trị biểu thức $S=z_{1}^{2019}+z_{2}^{2019}+z_{3}^{2019}$
Cho ba số phức ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$ thỏa mãn hệ $\left\{ \begin{align}& \left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=\left| {{z}_{3}} \right|=1 \\& {{z}_{1}}+{{z}_{2}}+{{z}_{3}}=1 \\\end{align} \right.$. Tính giá trị biểu thức $S=z_{1}^{2019}+z_{2}^{2019}+z_{3}^{2019}$.
A. $S=-1$. B. $S={{2}^{2019}}$. C. $S=1$. D. $S={{2}^{-2019}}$.
Lời giải
Chọn C
Đặt $\left( 1 \right):\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=\left| {{z}_{3}} \right|=1$, $\left( 2 \right):{{z}_{1}}+{{z}_{2}}+{{z}_{3}}=1$.
Gọi $A$, $B$, $C$ lần lượt là điểm biểu diễn số phức ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$.
Từ $\left( 1 \right)\Rightarrow OA=OB=OC=1\Rightarrow $ Đường tròn $\left( C \right)$ tâm $O$, bán kính $R=1$ ngoại tiếp $\Delta ABC$.
Gọi $G$, $H$ lần lượt là trọng tâm, trực tâm $\Delta ABC$.
Vì $G$ là điểm biểu diễn số phức $\frac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}$ mà $\overrightarrow{OH}=3.\overrightarrow{OG}$ nên từ $\left( 2 \right)\Rightarrow H\left( 1\,;\,0 \right)$.
Dễ thấy $H\in \left( C \right)$ nên $\Delta ABC$ vuông.
Giả sử $\Delta ABC$ vuông tại $C\Rightarrow C\left( 1\,;\,0 \right)\Rightarrow {{z}_{3}}=1$.
$\Rightarrow {{z}_{1}}+{{z}_{2}}=0\Rightarrow {{z}_{1}}=-{{z}_{2}}\Rightarrow z_{1}^{2019}=-z_{2}^{2019}\Rightarrow z_{1}^{2019}+z_{2}^{2019}=0$.
Vậy $S=1$.
Câu 5: Có bao nhiêu số phức $z$ thỏa mãn điều kiện
Có bao nhiêu số phức $z$ thỏa mãn ${{\left| z \right|}^{2}}=\left| z+\overline{z} \right|+\left| z-\overline{z} \right|$ và ${{z}^{2}}$ là số thuần ảo
A. $4$ B. $2$ C. $3$ D. $5$
Lời giải
Gọi số phức $z=a+bi$, $a,b\in \mathbb{R}$.
Ta có ${{\left| z \right|}^{2}}=\left| z+\overline{z} \right|+\left| z-\overline{z} \right|\Leftrightarrow {{a}^{2}}+{{b}^{2}}=\left| 2a \right|+\left| 2bi \right|$
$\Leftrightarrow {{a}^{2}}+{{b}^{2}}=2\left| a \right|+2\left| b \right|\,\,\left( 1 \right)$.
Lại có ${{z}^{2}}={{\left( a+bi \right)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi$ là số thuần ảo, suy ra ${{a}^{2}}-{{b}^{2}}=0\Leftrightarrow a=\pm b$
Trường hợp 1: $a=b$ thay vào $\left( 1 \right)$ ta được:
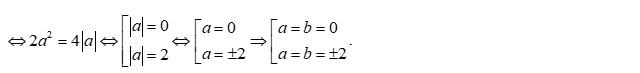
Trường hợp 2: $a=-b$ thay vào $\left( 1 \right)$ ta được:
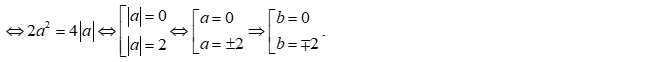
Vậy có $5$ số phức thỏa mãn bài toán là $z=0$, $z=2\pm 2i$, $z=-2\pm 2i$.
Câu 6: Tính tổng của các phần tử của tập $S$
Gọi $S$ là tập hợp các số thực $m$ sao cho với mỗi $m\in S$ có đúng một số phức thỏa mãn $\left| z-m \right|=6$ và $\frac{z}{z-4}$ là số thuần ảo. Tính tổng của các phần tử của tập $S$.
A. $10.$ B. $0.$ C. $16.$ D. $8.$
Lời giải
Cách 1:
Gọi $z=x+iy$ với $x,y\in \mathbb{R}$ ta có $\frac{z}{z-4}=\frac{x+iy}{x-4+iy}=\frac{\left( x+iy \right)\left( x-4-iy \right)}{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}=\frac{x\left( x-4 \right)+{{y}^{2}}-4iy}{{{\left( x-4 \right)}^{2}}+{{y}^{2}}}$
là số thuần ảo khi $x\left( x-4 \right)+{{y}^{2}}=0\Leftrightarrow {{\left( x-2 \right)}^{2}}+{{y}^{2}}=4$
Mà $\left| z-m \right|=6\Leftrightarrow {{\left( x-m \right)}^{2}}+{{y}^{2}}=36$

Ycbt $\Leftrightarrow 4-{{\left( \frac{36-{{m}^{2}}}{4-2m}-2 \right)}^{2}}=0$$\Leftrightarrow 2=\frac{36-{{m}^{2}}}{4-2m}-2$ hoặc $-2=\frac{36-{{m}^{2}}}{4-2m}-2$
$\Leftrightarrow m=10$ hoặc $m=-2$ hoặc $m=\pm 6$
Vậy tổng là $10-2+6-6=8$.
Câu 7: Tính tổng của các phần tử của $S$
Gọi $S$ là tập hợp các số phức $z$ thỏa mãn điều kiện ${{z}^{4}}=\left| z \right|$. Số phần tử của $S$ là
A. $7$. B. $6$. C. $5$. D. $4$.
Lời giải
Chọn C
Gọi $z=a+bi$, $\left( a,\,b\in \mathbb{R} \right)$ thì $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$ và
${{z}^{4}}={{\left( a+bi \right)}^{4}}={{\left( {{a}^{2}}-{{b}^{2}}+2abi \right)}^{2}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}-4{{a}^{2}}{{b}^{2}}+4ab\left( {{a}^{2}}-{{b}^{2}} \right)i$.
Ta có ${{z}^{4}}=\left| z \right|$$\Leftrightarrow {{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}-4{{a}^{2}}{{b}^{2}}+4ab\left( {{a}^{2}}-{{b}^{2}} \right)i=\sqrt{{{a}^{2}}+{{b}^{2}}}$.
Suy ra $\left\{ \begin{align}& 4ab\left( {{a}^{2}}-{{b}^{2}} \right)=0,\left( 1 \right) \\& {{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}-4{{a}^{2}}{{b}^{2}}=\sqrt{{{a}^{2}}+{{b}^{2}}},\left( 2 \right) \\\end{align} \right.$
Xét $\left( 1 \right)\Leftrightarrow \left[ \begin{align}& a=0 \\& b=0 \\& {{a}^{2}}={{b}^{2}} \\\end{align} \right.$.
Với $a=0$ thì từ $\left( 2 \right)\Rightarrow {{b}^{4}}=\left| b \right|\Rightarrow b=0,b=1,b=-1$ ta được $z=0;z=i;z=-i$.
Với $b=0$ thì từ $\left( 2 \right)\Rightarrow {{a}^{4}}=\left| a \right|\Rightarrow a=0,a=1,a=-1$ ta được $z=0;\,z=1;\,z=-1$.
Với ${{a}^{2}}={{b}^{2}}$ thì từ $\left( 2 \right)\Rightarrow -4{{a}^{4}}=\sqrt{2{{a}^{2}}}=\left| a \right|\sqrt{2}\Rightarrow a=0$,$b=0$$z=0$ ta được $z=0$.
Vậy $S=\left\{ 0;\,1;\,-1;\,\,i;\,-i \right\}$.
Câu 8: Tính tổng của các phần tử của $S$
Gọi $S$ là tập tất cả các giá trị thực của $m$ để tồn tại 4 số phức $z$ thỏa mãn $\left| z+\overline{z} \right|+\left| z-\overline{z} \right|=2$ và $z\left( \overline{z}+2 \right)-\left( z+\overline{z} \right)-m$ là số thuần ảo. Tổng các phần tử của $S$ là
A. $1$. B. $\frac{1}{\sqrt{2}}$. C. $\frac{3}{2}$. D. $\frac{3}{\sqrt{2}}$.
Lời giải
Chọn C
*) $z=x+yi$, $\forall x\,,\,y\in \mathbb{R}$ $\Rightarrow \left| z+\overline{z} \right|+\left| z-\overline{z} \right|=2$$\Leftrightarrow \left| 2x \right|+\left| 2yi \right|=2$$\Leftrightarrow \left| x \right|+\left| y \right|=1$.
*) $z\left( \overline{z}+2 \right)-\left( z+\overline{z} \right)-m$$=x{}^{2}+{{y}^{2}}+2yi-m$ là số thuần ảo $\Leftrightarrow {{x}^{2}}+{{y}^{2}}=m$$\left( m>0 \right)$.
Để tồn tại 4 số phức $z$ thì hệ phương trình $\left\{ \begin{align}& \left| x \right|+\left| y \right|=1 \\& {{x}^{2}}+{{y}^{2}}=m \\ \end{align} \right.$ có 4 nghiệm phân biệt.
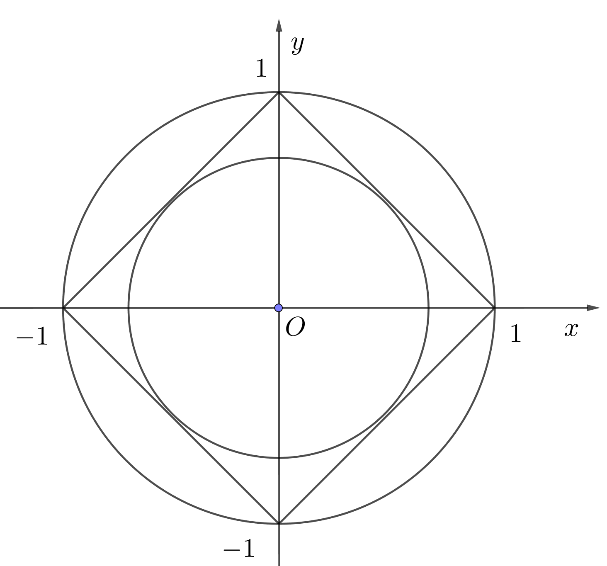
Hệ có 4 nghiệm thì đường tròn tâm $O$ bán kính $\sqrt{m}$ phải cắt các đường thẳng $\left| x \right|+\left| y \right|=1$ tại 4 điểm phân biệt.
Các đường thẳng $\left| x \right|+\left| y \right|=1$ đôi một cắt nhau tạo thành 1 hình vuông như trên đồ thị.
Để đường tròn $\left( C \right)$: ${{x}^{2}}+{{y}^{2}}=m$ cắt các đường thẳng $\left| x \right|+\left| y \right|=1$ tại 4 điểm thì đường tròn sẽ là đường tròn nội tiếp hoặc ngoại tiếp hình vuông với các bán kính tương ứng $r=\frac{1}{\sqrt{2}}$ và bán kính $R=1$. Hay $\left[ \begin{align}m=\frac{1}{2} \\ m=1 \\\end{align} \right.$. Suy ra tổng các giá trị $m$ cần tìm là $\frac{3}{2}$.
Xem thêm:
Tổng hợp các công thức số phức chi tiết và đầy đủ
Cách bấm máy tính số phức các dạng từ A-Z
Lý thuyết và bài tập mẫu số phức chi tiết nhất
Lý thuyết và bài tập của số phức liên hợp
