Trong bài viết ngày hôm nay, Khoa Cử chúng tôi muốn đem đến cho các bạn một dạng toán rất hay trong chương trình toán lớp 11 đó chính là về bài 3 đường thẳng và mặt phẳng song song rất đầy đủ và chi tiết cho các bạn tham khảo. Với những thông tin được Khoa cử chúng tôi chia sẽ về giáo án đường thẳng và mặt phẳng song song, bài giảng đường thẳng và mặt phẳng song song cũng như bài tập về đường thẳng và mặt phẳng song song bên dưới đây hy vọng sẽ hỗ trợ cho bạn học tốt môn Toán Hình Học lớp 11 nhé!
I. LÝ THUYẾT VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
1. Định nghĩa đường thẳng và mặt phẳng song song
Vị trí tương đối của đường thẳng và mặt phẳng.
– Đường thẳng có ít nhất 2 điểm chung với mặt phẳng (đường thẳng nằm trong mặt phẳng)

– Đường thẳng có 1 điểm chung với mặt phẳng (đường thẳng cắt mặt phẳng)
– Đường thẳng không có điểm chung với mặt phẳng (đường thẳng nằm trong mặt phẳng)
Định nghĩa
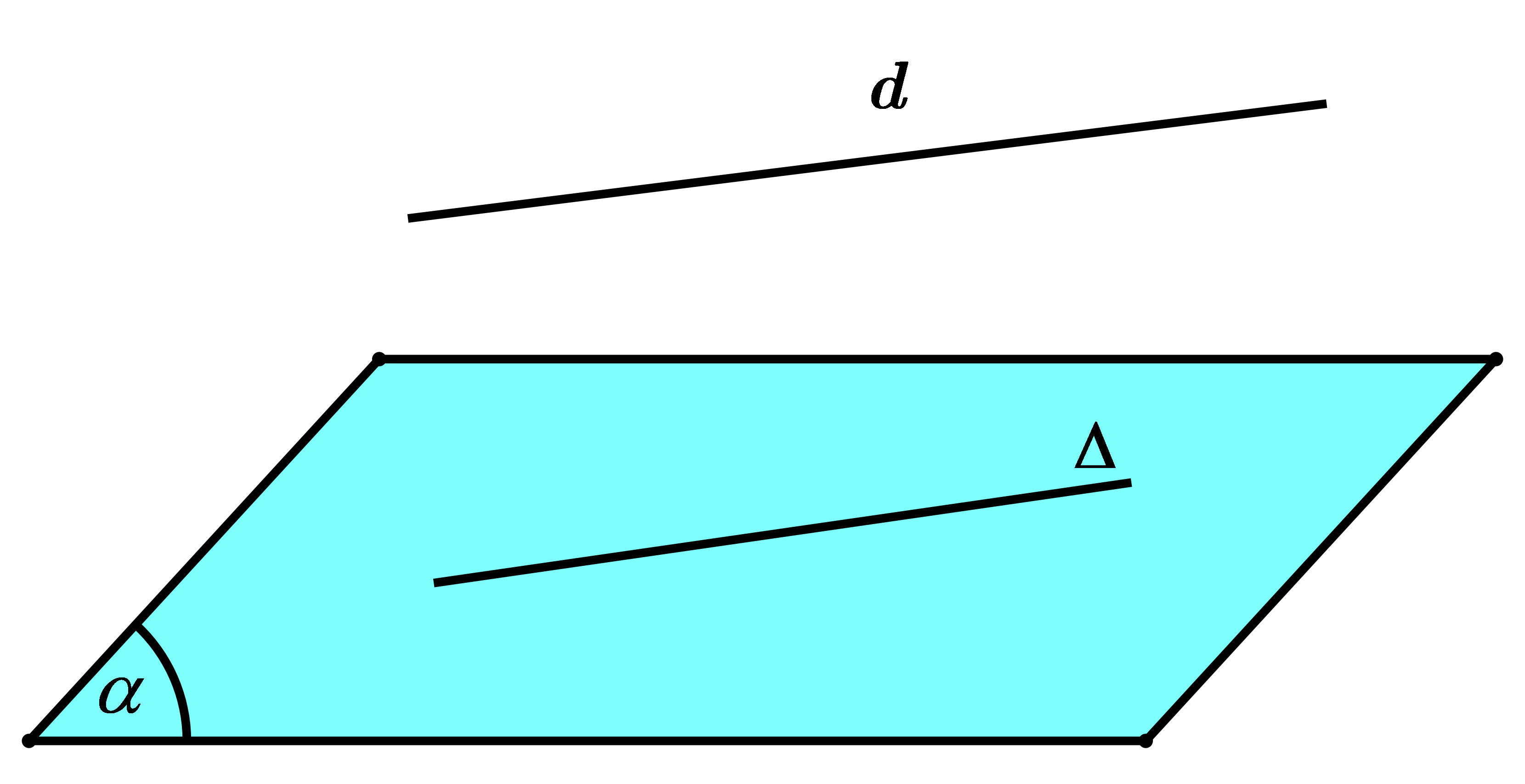
Đường thẳng $d$ gọi là song song với mặt phẳng $\left( \alpha \right)$ nếu đường thẳng $d$ không có điểm chung với mặt phẳng $\left( \alpha \right).$
$d//\left( \alpha \right)\Leftrightarrow d\cap \left( \alpha \right)=\varnothing $

2. Định lý
Định lý 1: Nếu đường thẳng $d$ không nằm trong mặt phẳng $\left( \alpha \right)$và song song với một đường thẳng nào đó nằm trong mặt phẳng $\left( \alpha \right)$ thì $d$ song song với mặt phẳng $\left( \alpha \right).$
$\left. \begin{align} & d//d’ \\ & d’\subset \left( \alpha \right) \\\end{align} \right\}\to d//\left( \alpha \right)$

3. Hệ quả
– Nếu 1 đường thẳng song song với 1 mặt phẳng nào đó thì nó song song với 1 đường thẳng nào đó nằm trong mặt phẳng đó.
Chú ý: không có tích chất sau đây
Hai đường thẳng cùng song song với 1 mặt phẳng thì chúng song song với nhau.
$\left. \begin{align} & a//\left( \alpha \right) \\ & b//\left( \alpha \right) \\\end{align} \right\}\to a//b$
Hai mặt phẳng cùng song song với 1 đường thẳng thì chúng song song với nhau.
$\left. \begin{align} & a//\left( \alpha \right) \\ & a//\left( \beta \right) \\\end{align} \right\}\to \left( \alpha \right)//\left( \beta \right)$
III. CÁC DẠNG TOÁN THƯỜNG GẶP
DẠNG 1. BÀI TOÁN CHỨNG MINH ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
$\left\{ \begin{align} & d\text{// }\!\!\Delta\!\!\text{ } \\ & d\not\subset \left( \alpha \right) \\ & \text{ }\!\!\Delta\!\!\text{ }\subset \left( \alpha \right) \\\end{align} \right.\Rightarrow d\text{//}\left( \alpha \right)$.
DẠNG 2. XÁC ĐỊNH GIAO TUYẾN CỦA 2 MẶT PHẲNG
Phương pháp:
Để tìm giao tuyến của 2 mặt phẳng, ngoài phương pháp “Tìm 2 điểm chung của 2 mặt phẳng”, ta sử dụng định lí về giao tuyến như sau:
- Bước 1: Chỉ ra rằng $\left( \alpha \right)$, $\left( \beta \right)$ lần lượt chứa hai đường thẳng song song $a$ và $b$.
- Bước 2: Tìm một điểm chung $M$của hai mặt phẳng.
- Bước 3: Khi đó $\left( \alpha \right)\cap \left( \beta \right)=Mx\text{//}a\text{//}b$.
DẠNG 3. THIẾT DIỆN ĐAI QUA MỘT ĐIỂM VÀ SONG SONG VỚI MỘT ĐƯỜNG THẲNG
Định nghĩa thiết diện: Thiết diện (mặt cắt) là một đa giác phẳng thu được khi cắt một khối chóp bằng một mặt phẳng. (Các cạnh của đa giác thu được là các đoạn giao tuyến của mặt phẳng với mặt bên hoặc mặt đáy của hình chóp).
Phương pháp: Tìm thiết diện của một hình chóp với một mặt phẳng $\left( P \right)$:
- Bước 1: Từ điểm chung có sẵn, xác định giao tuyến đầu tiên của $\left( P \right)$ với một mặt của hình chóp (có thể là mặt phẳng trung gian).
- Bước 2: Cho giao tuyến vừa tìm được cắt các cạnh của mặt đó của hình chóp, ta sẽ được các điểm chung mới của $\left( P \right)$ với các mặt khác. Từ đó xác định được giao tuyến với các mặt này.
- Bước 3: Tiếp tục như trên tới khi các giao tuyến khép kín ta được thiết diện.
Chú ý:
+ Thiết diện của một khối chóp là một đa giác bao quanh viền ngoài khối chóp, không có đường thẳng nào đâm xuyên bên trong khối chóp đó.
+ Có thể tìm thiết diện bằng phương pháp dựng giao điểm.
II. BÀI TẬP MẪU VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG
Bài tập 1: Tìm $x$ để $GE\text{//}\left( SBC \right)$
Cho hình chóp $S.ABCD$ có đáy là hình thang với $AD\text{//}BC$. Gọi $G$là trọng tâm của tam giác $SAD$; $E$ là điểm thuộc đoạn $AC$ sao cho $EC=xEA,\,\,\left( x>0 \right)$. Tìm $x$ để $GE\text{//}\left( SBC \right)$ .
Lời giải
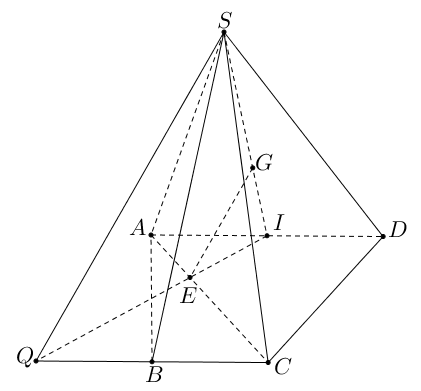
Gọi $I$ là trung điểm của cạnh $AD$.
Trong mặt phẳng $\left( ABCD \right)$ giả sử $IE$ và $BC$ cắt nhau tại điểm $Q$.
Dễ thấy $SQ=\left( IGE \right)\cap \left( SBC \right)$.
Do đó : $GE\text{//}\left( SBC \right)$ $\Leftrightarrow GE\text{//}SQ$ $\Leftrightarrow \frac{IE}{IQ}=\frac{IG}{IS}$ $\Rightarrow \frac{IE}{IQ}=\frac{1}{3}$ (1).
Mặt khác tam giác $EIA$ đồng dạng với tam giác $EQC$ nên $\frac{EI}{EQ}=\frac{EA}{EC}=\frac{EA}{xEA}=\frac{1}{x}$ suy ra $EQ=x.EI$.
$\Rightarrow \frac{IE}{IQ}=\frac{IE}{IE+EQ}=\frac{IE}{IE+x.IE}=\frac{1}{1+x}$ (2).
Từ (1) và (2) $\Rightarrow \frac{1}{1+x}=\frac{1}{3}$ $\Leftrightarrow x=2$.
Vậy $GE\text{//}\left( SBC \right)$ $\Leftrightarrow x=2$.
Bài tập 2: Tìm hệ thức liên hệ giữa $x$ và $y$ để $MN\text{//}\left( SAD \right)$
Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M$, $N$ lần lượt là các điểm thuộc cạnh$SB$ và đoạn $AC$ sao cho $\frac{BM}{MS}=x$ và $\frac{NC}{NA}=y$, $\left( 0<x,\,\,y\ne 1 \right)$. Tìm hệ thức liên hệ giữa $x$ và $y$ để $MN\text{//}\left( SAD \right)$.
Lời giải
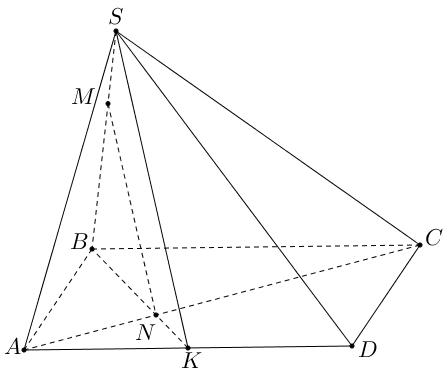
Trong mặt phẳng $\left( ABCD \right)$ giả sử $BN$ và $AD$ cắt nhau tại điểm $K$.
Dễ thấy $SK=\left( BMN \right)\cap \left( SAD \right)$.
Do đó : $MN\text{//}\left( SAD \right)$ $\Leftrightarrow MN\text{//}SK$ $\Leftrightarrow \frac{BM}{MS}=\frac{BN}{NK}$ (1)
Mặt khác tam giác $NCB$ đồng dạng với tam giác $NAK$ $\Rightarrow \frac{BN}{NK}=\frac{CN}{NA}$ (2).
Từ (1) và (2) $\Rightarrow \frac{BM}{MS}=\frac{NC}{NA}$ $\Leftrightarrow x=y$.
Vậy $MN\text{//}\left( SAD \right)$ $\Leftrightarrow x=y$.
Xem thêm: Bài tập hai mặt phẳng song song có lời giải chi tiết
Bài tập 3: Tính tỉ số $k=\frac{BC}{BD}$ khi $O{O}’\text{//}\left( BCD \right)$
Cho tứ diện $ABCD$ có $AB=2AC=3AD$. Gọi $O$, ${O}’$ lần lượt là tâm đường tròn nội tiếp của các tam giác $ABC$ và $ABD$. Tính tỉ số $k=\frac{BC}{BD}$ khi $O{O}’\text{//}\left( BCD \right)$.
Lời giải

Trong mặt phẳng $\left( ABC \right)$: Giả sử $AO$ và $BC$ cắt nhau tại điểm $M$.
Trong mặt phẳng $\left( ABD \right)$: Giả sử $A{O}’$ và $BD$ cắt nhau tại điểm $N$.
Ta có : $MN=\left( AO{O}’ \right)\cap \left( BCD \right)$.
Do đó : $O{O}’\text{//}\left( BCD \right)$ $\Leftrightarrow O{O}’\text{//}MN$ $\Leftrightarrow \frac{AO}{OM}=\frac{A{O}’}{{O}’N}$ (1)
Mặt khác theo tính chất đường phân giác ta có :
+ $\frac{AO}{OM}=\frac{AB}{BM}=\frac{AC}{CM}$$\Rightarrow \frac{AO}{OM}=\frac{AB+AC}{BM+CM}=\frac{AB+AC}{BC}$.
+ $\frac{A{O}’}{{O}’M}=\frac{AB}{BN}=\frac{AD}{DN}$$\Rightarrow \frac{A{O}’}{{O}’M}=\frac{AB+AD}{BN+DN}=\frac{AB+AD}{BD}$.
Vậy đẳng thức (1) $\Leftrightarrow $ $\frac{AB+AC}{BC}=\frac{AB+AD}{BD}$$\Leftrightarrow \frac{BC}{BD}=\frac{AB+AC}{AB+AD}$.
Theo giả thiết : $AB=2AC=3AD$ $\Rightarrow \frac{BC}{BD}=\frac{\frac{3}{2}AB}{\frac{4}{3}AB}=\frac{9}{8}$.
Kết luận : $O{O}’\text{//}\left( BCD \right)$ $\Leftrightarrow k=\frac{BC}{BD}=\frac{9}{8}$.
Bài tập 4: Chứng minh $MN$ song song với giao tuyến của hai mặt phẳng $\left( SAD \right)$ và $\left( SBC \right)$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. $Sx$ là giao tuyến của hai mặt phẳng $\left( SAD \right)$ và $\left( SBD \right)$. $M$, $N$ lần lượt là trung điểm của $AB$ và $DC$. Chứng minh $MN$ song song với giao tuyến của hai mặt phẳng $\left( SAD \right)$ và $\left( SBC \right)$.
Lời giải

Dễ thấy $S$ là điểm chung của mặt phẳng $\left( SAD \right)$ và $\left( SBC \right)$
Ta có: $\left\{ \begin{align} & AD\subset \left( SAD \right) \\ & BC\subset \left( SBC \right) \\ & AD\text{//}BC \\\end{align} \right.$ $\Rightarrow \left( SAD \right)\cap \left( SBC \right)=Sx\text{//}AD\text{//}BC$
Do $\left\{ \begin{align} & AD\text{//}MN\text{//}BC \\ & MN\not\subset \left( SAD \right);\,MN\not\subset \left( SBC \right) \\\end{align} \right.$ $\Rightarrow MN\text{//}\left( SAD \right)$ và $MN\text{//}\left( SBC \right)$.
Mặt khác $Sx=\left( SAD \right)\cap \left( SBC \right)$ $\Rightarrow MN\text{//}Sx$.
Bài tập 5: Tìm giao tuyến của hai mặt phẳng $\left( DBC \right)$ và $\left( DMN \right).$
Cho tứ diện ${ABCD}$ Gọi $M,\,\,N$ tương ứng là $AB,\,\,AC.$Tìm giao tuyến của hai mặt phẳng $\left( DBC \right)$ và $\left( DMN \right).$
Lời giải

${MN}$ là đường trung bình của tam giác ${ABC}$ nên $MN\text{//}BC.$
Ta có $\left\{ \begin{align} & MN//BC \\ & MN\subset \left( DMN \right) \\ & BC\subset \left( BCD \right) \\\end{align} \right.\Rightarrow \left( DMN \right)\cap \left( BCD \right)=\Delta ,$ với $\Delta$ đi qua $D,\,\,\Delta //BC.$
Bài tập 6:
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$. Gọi $M$ là trung điểm của $SB$,$N$ là điểm trên cạnh $BC$ sao cho $BN=2CN.$
a/ Chứng minh rằng: $OM\text{//}(SCD)$
b/ Xác định giao tuyến của $(SCD)$ và $(AMN)$.
Lời giải:

a/ Chứng minh $OM\text{//}(SCD)$.
Ta có $\left\{ \begin{align} & BM=\frac{1}{2}BS \\ & BO=\frac{1}{2}BD \\\end{align} \right.\Rightarrow OM\text{//}SD$.Mà $SD\subset (SCD)$, suy ra $OM\text{//}(SCD)$ (đpcm).
b/ Gọi $H=AN\cap CD$ (cùng nằm trong $(ABCD)$).
Suy ra $H$ là điểm chung thứ nhất của $(AMN)$ và $(SCD)$.
Ta có $I=AN\cap BD$, suy ra $IM\cap SD=K$ (cùng nằm trong $(SBD)$); nên $K$ là điểm chung thứ hai của $(AMN)$ và $(SCD)$.
Do đó $HK$ là giao tuyến của hai mặt phẳng $(AMN)$ và $(SCD)$.
Bài tập 7: Tìm thiết diện là hình gì
Cho tứ diện $ABCD$, lấy điểm $M$là một điểm thuộc miền trong của tam giác $BCD$. Gọi $\left( \alpha \right)$ là mặt phẳng qua $M$và song song với $AC$ và $BD$. Hãy xác định thiết diện của mặt phẳng $\left( \alpha \right)$ với tứ diện $ABCD$. Thiết diện là hình gì ?
Lời giải

– $M$ là điểm chung của hai mặt phẳng $\left( \alpha \right)$ và $\left( BCD \right)$. Ta có $\left( \alpha \right)\text{//}BD$ nên giao tuyến của chúng qua $M$ và song song với $BD$, giao tuyến này cắt $BC$ tại $E$ và cắt $CD$ tại $F$.
– $E$ là điểm chung của hai mặt phẳng $\left( \alpha \right)$ và $\left( ABC \right)$. Ta có $\left( \alpha \right)\text{//}AC$ nên giao tuyến của chúng qua $E$ và song song với $AC$, giao tuyến này cắt $AB$ tại $H$.
– $H$ là điểm chung của hai mặt phẳng $\left( \alpha \right)$ và $\left( ABD \right)$. Ta có $\left( \alpha \right)\text{//}BD$ nên giao tuyến của chúng qua $H$ và song song với $BD$, giao tuyến này cắt $AD$ tại $G$.
$G$ và $F$ là hai điểm chung của hai mặt phẳng $\left( \alpha \right)$ và $\left( ACD \right)$. Vậy giao tuyến của chúng là $FG$.
Vì mặt phẳng $\left( \alpha \right)\text{//}AC$ nên giao tuyến $FG\text{//}AC$.
Kết luận: Thiết diện cần tìm là hình bình hành $EFGH$vì $EF\text{//}BD\text{//}HG$ và $HE\text{//}FG\text{//}AC$.
Bài tập 8:
Cho tứ diện $ABCD$. Trên cạnh $AD$ lấy trung điểm $M$, trên cạnh $BC$ lấy điểm $N$ bất kỳ. Gọi $\left( \alpha \right)$ là mặt phẳng chứa đường thẳng $MN$ và song song với $CD$.
a) Hãy xác định thiết diện của mặt phẳng $\left( \alpha \right)$ với tứ diện $ABCD$.
b) Xác định vị trí của $N$ trên $BC$ sao cho thiết diện là hình bình hành.
Lời giải
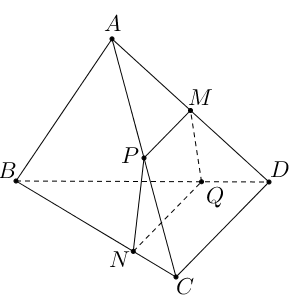
a) Xác định thiết diện của mặt phẳng $\left( \alpha \right)$ với tứ diện $ABCD$.
Ta có $\left\{ \begin{align} & \left( \alpha \right)\text{//}CD \\ & CD\subset \left( ACD \right) \\ & M\in \left( \alpha \right)\cap \left( ACD \right) \\\end{align} \right.$
$\Rightarrow \left( \alpha \right)\cap \left( ACD \right)=MP,\,\,\left( MP\text{//}CD,\,P\in AC \right)$ (1)
Ta có $\left\{ \begin{align} & \left( \alpha \right)\text{//}CD \\ & CD\subset \left( BCD \right) \\ & N\in \left( \alpha \right)\cap \left( ACD \right) \\\end{align} \right.$
$\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=NQ,\,\,\left( NQ\text{//}CD,\,Q\in BD \right)$ (2)
Và $\left( \alpha \right)\cap \left( ABD \right)=MQ$ (3)
$\left( \alpha \right)\cap \left( ABC \right)=PN$ (4)
Từ (1), (2) ta được : $MP\text{//}NQ$. Vậy thiết diện là hình thang $MNPQ$.
b) Xác định vị trí của $N$ trên $BC$ sao cho thiết diện là hình bình hành.
Ta có: $MP\text{//}NQ;\,\,MP=\frac{1}{2}CD$ ($MP$ là đường trung bình của tam giác $ACD$)
$MNPQ$ là hình bình hành $\Leftrightarrow \left\{ \begin{align} & MP\text{//}NQ \\ & MP=NQ \\\end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & MP\text{//}NQ \\ & MP=NQ=\frac{1}{2}CD \\\end{align} \right.$.
Do đó $N$ là trung điểm $BC$.
Vậy $N$ là trung điểm $BC$ thì $MPNQ$ là hình bình hành.
Bài tập 9:
Cho hình chóp $S.ABCD$. $M$, $N$ là hai điểm trên đoạn $AB$, $CD$. Mặt phẳng $\left( \alpha \right)$ qua $MN$ và song song với $SA$.
a) Xác định thiết diện của hình chóp với mặt phẳng $\left( \alpha \right)$.
b) Tìm điều kiện của $MN$ để thiết diện là hình thang.
Lời giải

a. Xác định thiết diện của hình chóp với mặt phẳng $\left( \alpha \right)$.
Ta có :$\left\{ \begin{align} & M\in \left( \alpha \right)\cap \left( SAB \right) \\ & \left( \alpha \right)\text{//}SA,SA\subset \left( SAB \right) \\\end{align} \right.$$\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MP$ (với $MP\text{//}SA,P\in SB)$.
Gọi $R=MN\cap AC\,\,\left( MN,AC\subset \left( ABCD \right) \right)$.
Ta có:$\left\{ \begin{align} & R\in \left( \alpha \right)\cap \left( SAC \right) \\ & \left( \alpha \right)\text{//}SA,SA\subset \left( SAC \right) \\\end{align} \right.$$\Rightarrow \left( \alpha \right)\cap \left( SAC \right)=RQ$ (với $RQ\text{//}SA,Q\in SC$)
Vậy thiết diện của hình chóp với mặt phẳng $\left( \alpha \right)$là tứ giác $MPQN$
b. Tìm điều kiện của $MN$để thiết diện là hình thang.
Ta có $MPQN$là hình thang $\Rightarrow \left[ \begin{align} & MP\text{//}QN\,\,\left( 1 \right) \\ & MN\text{//}PQ\,\,\left( 2 \right) \\\end{align} \right.$
Xét (1) ta có $\left\{ \begin{align} & SA\text{//}MP \\ & MP\text{//}QN \\\end{align} \right.$$\Rightarrow SA\text{//}QN$.
Do đó: $\left\{ \begin{align} & SA\text{//}QN \\ & QN\subset \left( SCD \right) \\\end{align} \right.$$\Rightarrow SA\text{//}\left( SCD \right)$ (vô lí).
Xét (2) ta có $\left\{ \begin{align} & BC=\left( ABCD \right)\cap \left( SBC \right) \\ & MN\subset \left( ABCD \right),PQ\subset \left( SBC \right) \\\end{align} \right.\Rightarrow MN\text{//}BC$ .
Ngược lại, nếu $MN\text{//}BC$ thì $\left\{ \begin{align} & PQ=\left( \alpha \right)\cap \left( SBC \right) \\ & MB\subset \left( \alpha \right),BC\subset \left( SBC \right) \\\end{align} \right.\Rightarrow MN\text{//}PQ$.
Vậy để thiết diện là hình thang thì $MN\text{//}BC$.
Xem thêm:
