Trong bài viết ngày hôm nay, Khoa Cử chúng tôi muốn đem đến cho các bạn một dạng toán rất hay trong chương trình toán lớp 11 đó chính là về phép dời hình và phép đồng dạng trong mặt phẳng rất đầy đủ và chi tiết cho các bạn tham khảo. Với những thông tin được Khoa cử chúng tôi chia sẽ về khái niệm về phép dời hình và hai hình bằng nhau hay phép đồng dạng là một phép dời hình cũng như bài tập phép dời hình lớp 11 bên dưới đây hy vọng sẽ hỗ trợ cho bạn học tốt môn Toán lớp 11 và đạt được thành tích cao trong học tập nhé!
I. LÝ THUYẾT VỀ PHÉP DỜI HÌNH
- Định nghĩa
Hai hình $\left( H \right)$ và $\left( G \right)$ gọi là hai hình bằng nhau nếu phép dời hình biến hình này thành hình kia và ngược lại.
- Định nghĩa rời hình là gì
Nếu thực hiện liên tiếp 2 phép dời hình thì được 1 phép dời hình
II. BÀI TẬP MẪU VỀ PHÉP DỜI HÌNH
Bài tập 1: Tìm phép dời hình biến $\Delta AEI$ thành $\Delta FCH$
Cho hình chữ nhật $ABCD$, gọi $E,F,H,I$ lần lượt là trung điểm của $AB,CD,BC,EF$. Tìm phép dời hình biến $\Delta AEI$ thành $\Delta FCH$ ?
Giải
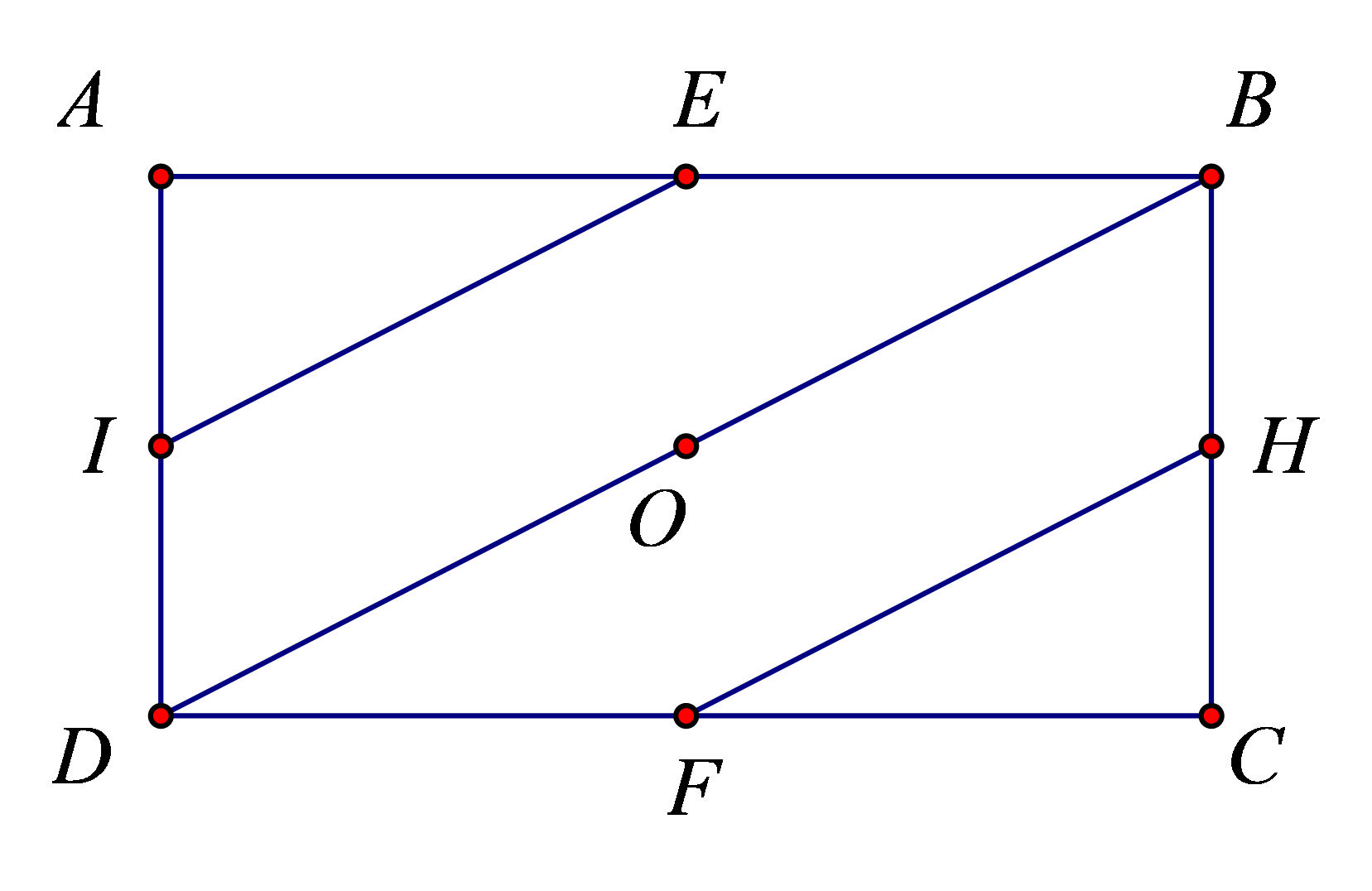
Gọi $O$ là tâm hình chữ nhật, phép dời hình là phép đối xứng tâm $O$ biến $\Delta AEI$ thành $\Delta CFH$.
Bài tập 2: Tìm phép dời hình biến $\Delta AMQ$ thành $\Delta EBC$
Cho hình chữ nhật $ABCD$, có $AB=2BC$. Gọi $M,N,P,Q,E$ lần lượt là trung điểm của $AB$, $CD$, $BC$, $AD$ và $MB$. Tìm phép dời hình biến $\Delta AMQ$ thành $\Delta EBC$ ?
Giải
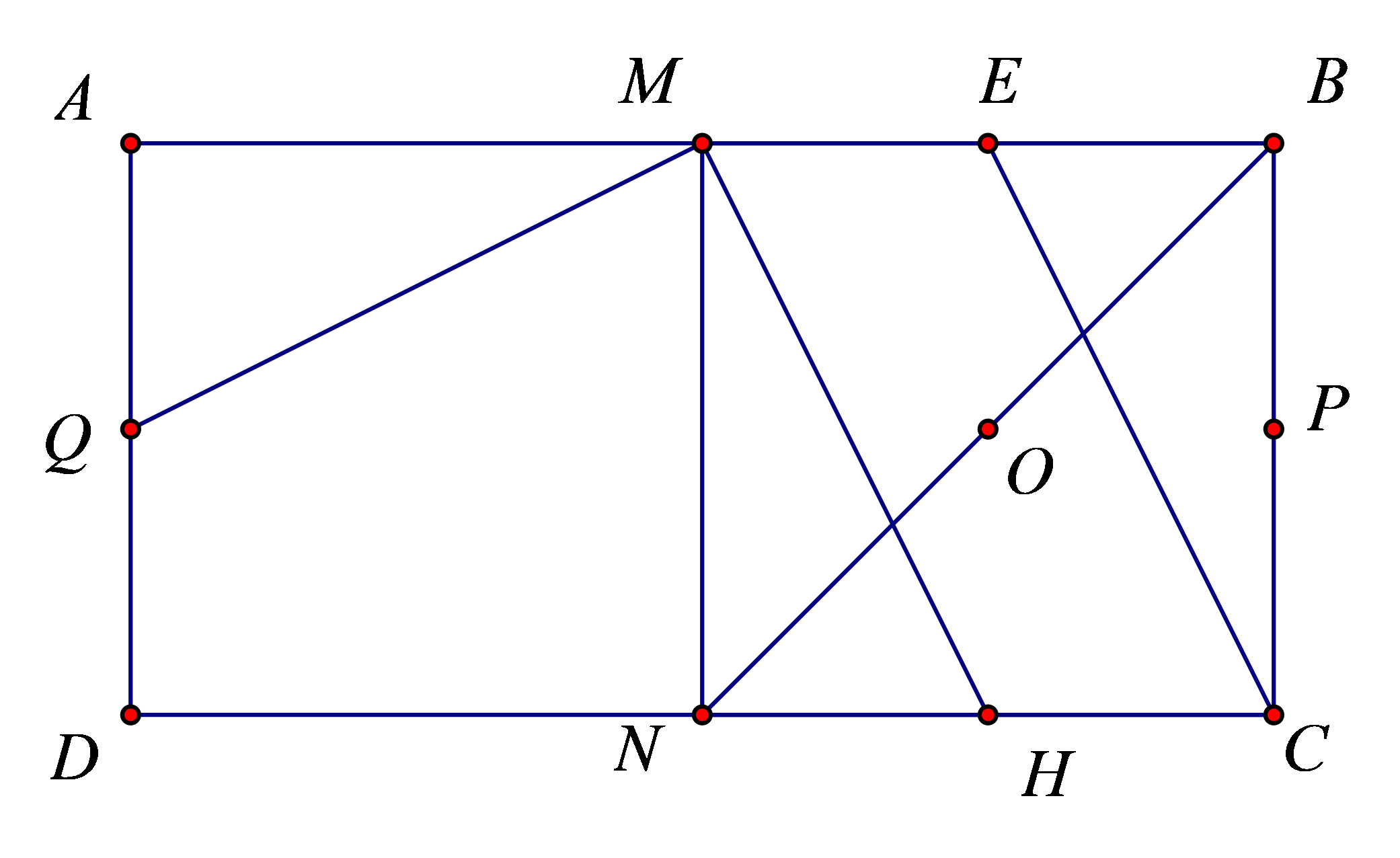
Gọi $H,O$ lần lượt là trung điểm của $NC,AB$, khi đó phép dời hình cần tìm là
$\Delta MAQ\xrightarrow{{{Q}_{\left( M,90{}^\circ \right)}}}\Delta MNH\xrightarrow{{{}_{O}}}\Delta CBE$
Xem thêm: Lý thuyết và bài tập mẫu phép đồng dạng
Bài tập 3:
Trong mặt phẳng tọa độ $Oxy$ cho đường tròn $\left( C \right):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4$. Nếu thực hiện liên tiếp phép tịnh tiến theo véc tơ $\overrightarrow{v\,}\left( 2;3 \right)$và phép đối xứng trục $\left( \Delta \right):x-y-3=0$ thì đường tròn $(C)$ biến thành đường tròn nào?
Lời giải
Đường tròn $\left( C \right):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=4$có tâm $I(1;-2)$và bán kính $R=2$.
Gọi ${{C}_{1}}({{I}_{1}},{{R}_{1}})$ là ảnh của $C(I,R)$ qua phép ${{T}_{\overrightarrow{v}}}$
Ta có: ${{R}_{1}}=R=2\,,\,\,\,{{I}_{1}}={{T}_{\overrightarrow{v}}}(I)=(1+2;-2+3)=(3;1)$
nên $({{C}_{1}})$có phương trình: ${{(x-1)}^{2}}+{{(y-2)}^{2}}=4$
Gọi ${{C}_{2}}({{I}_{2}},{{R}_{2}})$ là ảnh của ${{C}_{1}}({{I}_{1}},{{R}_{1}})$qua phép ${{D}_{\Delta }}$
Ta có: ${{R}_{2}}={{R}_{1}}=2$
Phương trình đường thẳng ${{I}_{1}}{{I}_{2}}$ đi qua ${{I}_{1}}(3;1)$ nhận $\overrightarrow{u}(1;1)$ làm vecto pháp tuyến: $1.(x-3)+1.(y-1)=0\Leftrightarrow x+y-4=0$
Gọi $\left\{ M \right\}={{I}_{1}}{{I}_{2}}\cap \Delta $. $M(x;y)\Rightarrow \left\{ \begin{align} & x+y-4=0 \\ & x-y-3=0 \\\end{align} \right.$$\Leftrightarrow \left\{ \begin{align} & x=\frac{7}{2} \\ & y=\frac{1}{2} \\\end{align} \right.$$\Rightarrow M\left( \frac{7}{2};\frac{1}{2} \right)$
M là trung điểm của ${{I}_{1}}{{I}_{2}}\Rightarrow {{I}_{2}}\left( 2.\frac{7}{2}-3;2.\frac{1}{2}-1 \right)=\left( 4;0 \right)$
$({{C}_{2}})$có phương trình: ${{(x-4)}^{2}}+{{y}^{2}}=4$
Bài tập 4: Tìm Ảnh của đường tròn
Trong mặt phẳng tọa độ $Oxy$, cho đường tròn $\left( C \right):{{\left( x-7 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=4$. Ảnh của đường tròn qua việc thực hiện liên tiếp phép tịnh tiến theo véc tơ $\overrightarrow{v}=\left( 1;5 \right)$ và phép quay tâm $O$, góc quay $-{{45}^{\circ }}$ là
A. ${{\left( x+8 \right)}^{2}}+{{\left( y-8 \right)}^{2}}=4$. B. ${{x}^{2}}+{{\left( y-8\sqrt{2} \right)}^{2}}=4$.
C. ${{\left( x-8\sqrt{2} \right)}^{2}}+{{\left( y-8 \right)}^{2}}=4$. D. ${{\left( x-8\sqrt{2} \right)}^{2}}+{{y}^{2}}=4$.
Lời giải
Chọn D.
Gọi $I$ là tâm đường tròn và $2$ là ảnh của $8$khi thực hiện liên tiếp phép tịnh tiến theo véc tơ $9$ và phép quay tâm $8!+9!$, góc quay $72$.
Gọi $17$ là ảnh của $8!.9!$ khi thực hiện phép tịnh tiến theo véc tơ $C_{8}^{1}$.
Ta có$C_{9}^{1}$ nên $C_{8}^{1}.C_{9}^{1}=72$.
Gọi $5$ là ảnh của $3$ khi thực hiện phép quay tâm $8!$, góc quay $2.5!.3!$.
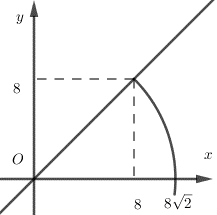
Suy ra $5!.3!$. Do đó $2.\left( 5!+3! \right)$là ảnh của $2!=2$ khi thực hiện liên tiếp phép tịnh tiến theo véc tơ $5!$ và phép quay tâm $3!$, góc quay $2.5!.3!$hay $-90{}^\circ $ là tâm của $-90{}^\circ $. Hơn nữa, phép quay và phép tịnh tiến đều bảo toàn khoảng cách nên $y=\frac{1-\sin x}{\cos x-1}$.
Vậy có $D=\mathbb{R}\backslash \left\{ k\pi ,k\in \mathbb{Z} \right\}$ phương trình là $M$.
Bài tập 5: Tìm ảnh của điểm N
Tìm ảnh của điểm $N\left( 2\,;\,-4 \right)$ qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm $O$ góc quay $-90{}^\circ $ và phép tịnh tiến theo vectơ $\overrightarrow{u}=\left( -1\,;\,2 \right)$.
A. $N’\left( -5\,;\,0 \right)$. B. $N’\left( -2\,;\,-4 \right)$. C. $N’\left( -4\,;\,-2 \right)$. D. $N’\left( 2\,;\,-4 \right)$.
Lời giải
Chọn A
Ảnh của điểm $N\left( 2\,;\,-4 \right)$ qua phép quay tâm $O$ góc quay $-90{}^\circ $ là ${{N}_{1}}\left( -4\,;\,-2 \right)$.
Ảnh của điểm ${{N}_{1}}\left( -4\,;\,-2 \right)$ qua phép tịnh tiến theo vectơ $\overrightarrow{u}\left( -1\,;\,2 \right)$ là $N’\left( -5\,;\,0 \right)$.
Vậy ảnh của điểm $N\left( 2\,;\,-4 \right)$ qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm $O$ góc quay $-{{90}^{0}}$ và phép tịnh tiến theo vectơ $\overrightarrow{u}\left( -1;2 \right)$ là $N’\left( -5;0 \right)$.
Bài tập 6: Viết phương trình đường tròn là ảnh của đường tròn $\left( C \right)$ thỏa mãn điều kiện
Trong mặt phẳng $\left( Oxy \right)$ cho đường tròn $\left( C \right):{{\left( x+2 \right)}^{2}}+{{\left( y-4 \right)}^{2}}=10.$ Viết phương trình đường tròn là ảnh của đường tròn $\left( C \right)$ qua phép biến hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vecto $\overrightarrow{v}=\left( 3;2 \right)$ và phép đối xứng trục $Oy$
A. ${{\left( x+1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=10$. B. ${{\left( x-1 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=10$.
C. ${{\left( x+1 \right)}^{2}}+{{\left( y-6 \right)}^{2}}=10$. D. ${{\left( x+5 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=10$.
Lời giải
Chọn C
Tâm $I\left( -2;4 \right)$, Gọi ${I}’={{T}_{\overrightarrow{v}}}\left( I \right)$. Ta có:
$\overrightarrow{I{I}’}=\overrightarrow{v}\Leftrightarrow \left( {{x}_{{{I}’}}}-{{x}_{I}};{{y}_{{{I}’}}}-{{y}_{I}} \right)=\left( 3;2 \right)\Leftrightarrow \left\{ \begin{matrix} {{x}_{{{I}’}}}-{{x}_{I}}=3 \\ {{y}_{{{I}’}}}-{{y}_{I}}=2 \\\end{matrix} \right.$$\Leftrightarrow \left\{ \begin{matrix} {{x}_{{{I}’}}}=1 \\ {{y}_{{{I}’}}}=6 \\\end{matrix} \right.$
Gọi ${I}”$ là ảnh của ${I}’$ qua phép đối xứng trục $Oy$. Khi đó: $\left\{ \begin{matrix} {{x}_{{{I}”}}}=-{{x}_{{{I}’}}}=-1 \\ {{y}_{{{I}”}}}={{y}_{{{I}’}}}=6 \\\end{matrix} \right.$
Bài tập 7: Tính độ dài đoạn A1M1
Cho $\Delta ABC$ và điểm M thỏa mãn $\overrightarrow{BM}=2\overrightarrow{CM}$. $F$ là phép dời hình. Gọi $F\left( A \right)={{A}_{1}};\,F\left( B \right)={{B}_{1}};\,F\left( C \right)={{C}_{1}};\,F\left( M \right)={{M}_{1}}$, biết $AB=4,\,\,BC=5,\,\,CA=6$. Độ dài đoạn ${{\text{A}}_{1}}{{M}_{1}}$ bằng:
A. $116$. B. $\sqrt{106}$. C. $57$. D. $74$.
Lời giải:
Đáp án B.
Theo tính chất phép dời hình $AM={{A}_{1}}{{M}_{1}}$
$\overrightarrow{BM}=2\overrightarrow{CM}\Leftrightarrow \overrightarrow{AM}-\overrightarrow{AB}=2\left( \overrightarrow{AM}-\overrightarrow{AC} \right)\Leftrightarrow \overrightarrow{AM}=2\overrightarrow{AC}-\overrightarrow{AB}$$\Rightarrow A{{M}^{2}}=4\text{A}{{C}^{2}}+A{{B}^{2}}-4\overrightarrow{AC}.\overrightarrow{AB}$ $\left( * \right)$
Ta có: $\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow B{{C}^{2}}=A{{C}^{2}}+A{{B}^{2}}-2\overrightarrow{AC}.\overrightarrow{AB}$
$\Rightarrow 2\overrightarrow{AC}.\overrightarrow{AB}=A{{C}^{2}}+A{{B}^{2}}-B{{C}^{2}}$, thế vào $\left( * \right)$ ta có: $A{{M}^{2}}=2\text{A}{{C}^{2}}-A{{B}^{2}}+2B{{C}^{2}}=72-16+50=106$ $\Rightarrow AM=\sqrt{106}$
Bài tập 8: Phép biến hình nào trong hai phép biến hình trên là phép dời hình
Cho hai phép biến hình: ${{F}_{1}}:\,M\left( x;y \right)\to M’\left( x+1;y-3 \right)$, ${{F}_{2}}:\,M\left( x;y \right)\to M’\left( -y;x \right)$. Phép biến hình nào trong hai phép biến hình trên là phép dời hình.
A. Chỉ phép biến hình ${{F}_{1}}$.
B. Chỉ phép biến hình ${{F}_{2}}$.
C. Cả hai phép biến hình ${{F}_{1}}$ và ${{F}_{1}}$.
D. Cả hai phép biến hình ${{F}_{1}}$ và ${{F}_{1}}$ đều không là phép dời hình.
Lời giải:
Đáp án C.
Xét hai điểm $\text{A}\left( {{x}_{A}};{{y}_{A}} \right)$ và $B\left( {{x}_{B}};{{y}_{B}} \right)$ qua hai phép biến hình ${{F}_{1}}$ và ${{F}_{2}}$. Với phép biến hình ${{F}_{1}}:$$A\to A’\left( {{x}_{A}}+1;{{y}_{A}}-3 \right)$; $B\to B’\left( {{x}_{B}}+1;{{y}_{B}}-3 \right)$ $\Rightarrow AB=A’B’=\sqrt{{{\left( {{x}_{B}}-{{x}_{A}} \right)}^{2}}+{{\left( {{y}_{B}}-{{y}_{A}} \right)}^{2}}}$
Tương tự với phép biến hình ${{F}_{2}}$thì $AB=A’B’$ nên ta chọn đáp án C
Xem thêm:
Tổng hợp bài tập phép dời hình lớp 11
