Trong bài viết ngày hôm nay, Khoa Cử chúng tôi muốn đem đến cho các bạn một dạng bài rất hay trong chương trình toán lớp 12 đó chính là dạng vị trí tương đối của 2 đường thẳng trong không gian rất đầy đủ và chi tiết cho các bạn tham khảo. Với những thông tin được Khoa cử chúng tôi chia sẽ giải đáp cho các bạn về xét vị trí tương đối của 2 đường thẳng, vị trí tương đối của 2 đường thẳng trong oxyz tính như thế nào? Trong bài dưới đây hy vọng sẽ hỗ trợ cho bạn học tốt môn Toán Hình lớp 12 nhé!
I. CÁCH GIẢI TÍNH KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
$\centerdot $ Khoảng cách từ điểm $M$ đến một đường thẳng $d$ qua điểm ${{M}_{\circ }}$ có véctơ chỉ phương ${{\vec{u}}_{d}}$ được xác định bởi công thức

Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia.
$\centerdot $ Khoảng cách giữa hai đường thẳng chéo nhau: $d$ đi qua điểm $M$ và có véctơ chỉ phương $\vec{u}$ và ${d}’$ đi qua điểm ${M}’$ và có véctơ chỉ phương ${\vec{u}}’$ là
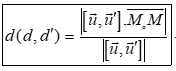
II. BÀI TẬP MẪU TÍNH KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
Bài tập 1: Tính Giá trị của $a+b+c$
Trong không gian $Oxyz,$ cho $2$ đường thẳng ${{d}_{1}}:\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-1}{2}$ và ${{d}_{2}}:\frac{x-1}{2}=\frac{y-1}{1}=\frac{z+2}{1}.$ Mặt phẳng $\left( P \right):x+ay+bz+c=0\left( c>0 \right)$ song song với ${{d}_{1}},{{d}_{2}}$ và khoảng cách từ ${{d}_{1}}$ đến $\left( P \right)$ bằng 2 lần khoảng cách từ ${{d}_{2}}$ đến $\left( P \right).$ Giá trị của $a+b+c$ bằng
A. $14$. B. $6$. C. $-4.$ D. $-6$.
Lời giải
Chọn A
Gọi ${{\vec{u}}_{1}}=\left( 1;\,1;\,2 \right)$, ${{\vec{u}}_{2}}=\left( 2;\,1;\,1 \right)$ lần lượt là một vectơ chỉ phương của ${{d}_{1}}$, ${{d}_{2}}$.
Gọi ${{\vec{n}}_{1}}=\left[ {{{\vec{u}}}_{1}},{{{\vec{u}}}_{2}} \right]=\left( -1;\,3;\,-1 \right)$, có ${{\vec{n}}_{1}}$ cùng phương ${{\vec{n}}_{2}}=\left( 1;\,-3;\,1 \right)$.
$\vec{n}=\left( 1;\,a;\,b \right)$ là một vec-tơ chỉ phương của $\left( P \right)$.
Do $\left( P \right)$ song song với ${{d}_{1}},{{d}_{2}}$ nên chọn $\vec{n}=\left( 1;\,-3;\,1 \right)$.
Suy ra phương trình mặt phẳng $\left( P \right)$ có dạng: $x-3y+z+c=0$.
Lấy ${{M}_{1}}\left( 1;\,-2;\,1 \right)\in {{d}_{1}}$, ${{M}_{2}}\left( 1;\,1;\,-2 \right)\in {{d}_{2}}$
Có $d\left( {{d}_{1}};\left( P \right) \right)=2d\left( {{d}_{2}};\left( P \right) \right)$$\Leftrightarrow d\left( {{M}_{1}};\left( P \right) \right)=2d\left( {{M}_{2}};\left( P \right) \right)$
$\Leftrightarrow \frac{\left| 1-3\left( -2 \right)+1+c \right|}{\sqrt{11}}=2\frac{\left| 1-3-2+c \right|}{\sqrt{11}}$$\Leftrightarrow \left| 8+c \right|=2\left| -4+c \right|$$\Leftrightarrow \left[ \begin{align}& 8+c=2\left( -4+c \right) \\& 8+c=2\left( 4-c \right) \\\end{align} \right.$
$\Leftrightarrow \left[ \begin{align} & c=16\,\,\left( \text{nha }\!\!\ddot{\mathrm{a}}\!\!\text{ n} \right) \\ & c=0\,\,\,\,\left( \text{loa }\!\!\ddot{\mathrm{i}}\!\!\text{ i} \right) \\\end{align} \right.$.
Nên $\left( P \right):\,\,x-3y+z+16=0$, suy ra $a=-3$, $b=1$, $c=16$.
Vậy $a+b+c=14$.
Bài tập 2: Tính khoảng cách giữa hai đường thẳng đã cho
Trong không gian$Oxyz$, cho hai đường thẳng ${{d}_{1}}:\frac{x-1}{2}=\frac{y+2}{-1}=\frac{z}{1}$ và ${{d}_{2}}:\left\{ \begin{align}& x=1+4t \\& y=-1-2t \\& z=2+2t \\\end{align} \right.$.
Khoảng cách giữa hai đường thẳng đã cho bằng?
A. $\frac{\sqrt{87}}{6}$. B. $\frac{\sqrt{174}}{6}$. C. $\frac{\sqrt{174}}{3}$. D. $\frac{\sqrt{87}}{3}$.
Lời giải
Chọn B
Ta có: Đường thẳng ${{d}_{1}}$ đi qua điểm $M(1;-2;0)$ và nhận $\overrightarrow{{{u}_{1}}}=\left( 2;-1;1 \right)$ làm VTCP.
Đường thẳng ${{d}_{2}}$ đi qua điểm $N(1;-1;2)$ và nhận $\overrightarrow{{{u}_{2}}}=\left( 4;-2;2 \right)$ làm VTCP.
Dễ thấy: $\overrightarrow{{{u}_{2}}}=2.\overrightarrow{{{u}_{1}}}$ nên đường thẳng ${{d}_{1}}$ song song hoặc trùng với đường thẳng ${{d}_{2}}$.
Lại có điểm $M\left( 1;-2;0 \right)\in {{d}_{1}}$ nhưng $M\left( 1;-2;0 \right)\notin {{d}_{2}}$ nên suy ra ${{d}_{1}}\text{ // }{{d}_{2}}$.
Vậy khoảng cách giữa hai đường thẳng đã cho bằng khoảng cách từ điểm $M\left( 1;-2;0 \right)$ đến
đường thẳng ${{d}_{2}}$.
$\text{d}\left( M\text{;}{{d}_{2}} \right)=\frac{\left| \overrightarrow{MN}\wedge \overrightarrow{{{u}_{2}}} \right|}{\left| \overrightarrow{{{u}_{2}}} \right|}$.
Ta có $\overrightarrow{MN}=\left( \text{0};\text{1};\text{2} \right)$,$\overrightarrow{MN}\wedge \overrightarrow{{{u}_{2}}}=\left( 6;8;-4 \right)$.
$\Rightarrow d\left( M;{{d}_{2}} \right)=\frac{\sqrt{{{6}^{2}}+{{8}^{2}}+{{\left( -4 \right)}^{2}}}}{\sqrt{{{4}^{2}}+{{\left( -2 \right)}^{2}}+{{2}^{2}}}}=\frac{\sqrt{174}}{6}\Rightarrow d({{d}_{1}};{{d}_{2}})=\frac{\sqrt{174}}{6}.$
Xem thêm: Lý thuyết và bài tập mẫu khoảng cách giữa hai đường thẳng
Bài tập 3: Tính Giá trị $h-k$
Trong không gian $Oxyz$cho ba đường thẳng $d:\frac{x}{1}=\frac{y}{1}=\frac{z+1}{-2},$${{\Delta }_{1}}:\frac{x-3}{2}=\frac{y}{1}=\frac{z-1}{1},$${{\Delta }_{2}}:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z}{1}$. Đường thẳng $\Delta $vuông góc với $d$ đồng thời cắt ${{\Delta }_{1}},{{\Delta }_{2}}$ tương ứng tại $H,K$ sao cho độ dài $HK$ nhỏ nhất. Biết rằng $\Delta $ có một vectơ chỉ phương $\overrightarrow{u}\left( h;k;1 \right).$ Giá trị $h-k$ bằng
A. $0.$ B. $4.$ C. $6.$ D. $-2.$
Lời giải
Chọn A
$H\in {{\Delta }_{1}}\Leftrightarrow H\left( 3+2t;t;1+t \right)$.
$K\in {{\Delta }_{2}}\Leftrightarrow K\left( 1+m;2+2m;m \right)$.
Ta có$\overrightarrow{HK}=\left( m-2t-2;2m-t+2;m-t-1 \right)$.
Đường thẳng $d$ có một VTCP là $\overrightarrow{{{u}_{d}}}=\left( 1;1;-2 \right)$.
$\Delta \bot d\Leftrightarrow $$\overrightarrow{{{u}_{d}}}.\overrightarrow{HK}=0$$\Leftrightarrow m-t+2=0\Leftrightarrow m=t-2\Rightarrow \overrightarrow{HK}=\left( -t-4;t-2;-3 \right).$
Ta có$H{{K}^{2}}={{\left( -t-4 \right)}^{2}}+{{\left( t-2 \right)}^{2}}+{{\left( -3 \right)}^{2}}=2{{\left( t+1 \right)}^{2}}+27\ge 27,\forall t\in \mathbb{R}$
$\Rightarrow minHK=\sqrt{27},$đạt được khi $t=-1$.
Khi đó ta có $\overrightarrow{HK}=\left( -3;-3;-3 \right)$, suy ra $\overrightarrow{u}\left( 1;1;1 \right)\Rightarrow h=k=1\Rightarrow h-k=0.$
Bài tập 4: Tính khoảng cách giữa $\left( \Delta \right)$ và $\left( P \right)$
Trong không gian $Oxyz$, cho mặt phẳng $\left( P \right):2x-y+2z-3=0$ và đường thẳng $\left( \Delta \right):\frac{x-1}{2}=\frac{y+1}{2}=\frac{x-1}{-1}$. Khoảng cách giữa $\left( \Delta \right)$ và $\left( P \right)$ là
A. $\frac{2}{3}$ B. $\frac{8}{3}$ C. $\frac{2}{9}$ D. $1$
Lời giải
Chọn A
Mặt phẳng $\left( P \right):2x-y+2z-3=0$ có véc tơ pháp tuyến là $\overrightarrow{n}=\left( 2;-1;2 \right)$.
Đường thẳng $\left( \Delta \right):\frac{x-1}{2}=\frac{y+1}{2}=\frac{z-1}{-1}$ có véc tơ chỉ phương là $\overrightarrow{u}=\left( 2;2;-1 \right)$ và đi qua điểm $M=\left( 1;-1;1 \right)$.
Ta có $\left\{ \begin{align}& \overrightarrow{n}.\overrightarrow{u}=0 \\ & M\notin \left( P \right) \\\end{align} \right.$suy ra $\left( \Delta \right)$ song song với $\left( P \right)$.
Khi đó $d\left( \left( \Delta \right),\left( P \right) \right)=d\left( M,\left( P \right) \right)=\frac{\left| 2+1+2-3 \right|}{\sqrt{{{2}^{2}}+{{2}^{2}}+{{\left( -1 \right)}^{2}}}}=\frac{2}{3}$.
Bài tập 5: Điểm nào sau đây thuộc mặt phẳng $\left( P \right)$
Trong không gian với hệ tọa độ $Oxyz$,cho đường thẳng $d:\left\{ \begin{align}& x=0 \\& y=3-t \\& z=t \\\end{align} \right.$.Gọi $\left( P \right)$là mặt phẳng chứa đường thẳng $d$ và tạo với mặt phẳng $\left( Oxy \right)$ một góc $45{}^\circ $.Điểm nào sau đây thuộc mặt phẳng $\left( P \right)$?
A. $M\left( 3\,;\,2\,;\,1 \right)$. B. $N\left( 3\,;\,2\,;\,-1 \right)$. C. $P\left( 3\,;\,-1\,;\,2 \right)$. D. $M\left( 3\,;\,-\,1;\,-2 \right)$.
Lời giải
Chọn A
Ta viết phương trình đường thẳng $d$:$\left\{ \begin{align} & x=0 \\ & y+z-3=0 \\\end{align} \right.$.
Mặt phẳng $\left( P \right)$chứa đường thẳng $d$nên có dạng: $mx+n\left( y+z-3 \right)=0,{{m}^{2}}+{{n}^{2}}\ne 0$
$\Leftrightarrow mx+ny+nz-3n=0\Rightarrow \left( P \right)$ có một véc tơ pháp tuyến là $\overrightarrow{{{n}_{P}}}=\left( m\,;\,n\,;\,n \right)$.
Mặt phẳng $\left( Oxy \right)$có một véc tơ pháp tuyến là $\overrightarrow{k}=\left( 0\,;\,0\,;\,1 \right)$.
Ta có: $\cos \left( \left( P \right);\left( Oxy \right) \right)=\left| \cos \left( \overrightarrow{{{n}_{P}}};\overrightarrow{k} \right) \right|\Leftrightarrow \cos 45{}^\circ =\frac{\left| \overrightarrow{{{n}_{P}}}.\overrightarrow{k} \right|}{\left| \overrightarrow{{{n}_{P}}} \right|.\left| \overrightarrow{k} \right|}\Leftrightarrow \frac{1}{\sqrt{2}}=\frac{\left| n \right|}{\sqrt{{{m}^{2}}+{{n}^{2}}+{{n}^{2}}}}$
$\Leftrightarrow \sqrt{{{m}^{2}}+2{{n}^{2}}}=\sqrt{2}\left| n \right|\Leftrightarrow {{m}^{2}}=0\Leftrightarrow m=0$.
Chọn $n=1\Rightarrow \left( P \right):y+z-3=0$.
Do đó: $M\left( 3 ;\,2\,;1 \right)\in \left( P \right)$.
Bình luận: Đối với những bài toán viết phương trình mặt phẳng chứa đường thẳng cho trước ta nên sử dụng khái niệm chùm mặt phẳng như sau: Mặt phẳng $\left( \alpha \right)$ qua giao tuyến của hai mặt phẳng $\left( P \right):{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z+{{d}_{1}}=0$và $\left( Q \right):{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z+{{d}_{2}}=0$ có phương trình dạng
$m\left( {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z+{{d}_{1}} \right)+n\left( {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z+{{d}_{2}} \right)=0,{{m}^{2}}+{{n}^{2}}\ne 0$.
Bài tập 6: Tính khoảng cách từ gốc tọa độ $\text{O}$ đến $\left( \Delta \right)$
Trong không gian với hệ tọa độ $\text{Ox}yz$, cho đường thẳng $\left( d \right):\frac{x-3}{1}=\frac{y-3}{3}=\frac{z}{2},$ mặt phẳng $\left( P \right):x+y-z+3=0$ và điểm $A\left( 1;2;-1 \right)$. Cho đường thẳng $\left( \Delta \right)$ đi qua $A$, cắt $\left( d \right)$ và song song với mặt phẳng $\left( P \right)$. Tính khoảng cách từ gốc tọa độ $\text{O}$ đến $\left( \Delta \right)$
A. $\sqrt{3}$. B. $\frac{16}{3}$. C. $\frac{2\sqrt{3}}{3}$. D. $\frac{4\sqrt{3}}{3}$.
Lời giải
Chọn D
Gọi $M=\left( \Delta \right)\cap \left( d \right)\Rightarrow M\left( t+3;3t+3;2t \right)\left( t\in R \right)\Rightarrow \overrightarrow{AM}=\left( t+2;3t+1;2t+1 \right)$.
Gọi $\overrightarrow{n}\left( 1;1;-1 \right)$ là vectơ pháp tuyến của mặt phẳng $\left( P \right)$.
Ta có $\left( \Delta \right)\,\,//\,\,\left( P \right)\Rightarrow \overrightarrow{AM}\bot \overrightarrow{n}\Leftrightarrow \overrightarrow{AM}.\overrightarrow{n}=0\Leftrightarrow t+2+3t+1-2t-1=0\Leftrightarrow t=-1$
$\Rightarrow \overrightarrow{AM}\left( 1;-2;-1 \right)\Rightarrow d\left( O;\Delta \right)=\frac{\left| \left[ \overrightarrow{AM},\overrightarrow{OA} \right] \right|}{\left| \overrightarrow{AM} \right|}=\frac{4\sqrt{3}}{3}$
Như vậy, bên trên là tất cả những thông tin cần thiết về cách giải cũng như bài tập mẫu về khoảng cách giữa hai đường thẳng chéo nhau mà các bạn không nên bỏ qua. Nếu như bạn có thắc mắc hay cần hỗ trợ thì đừng ngần ngại mà không liên hệ ngay với chúng tôi để nhận được sự trợ giúp sớm nhất nhé!
Xem thêm:
Lý thuyết và bài tập mẫu khoảng cách giữa hai đường thẳng
